Class 06 Project Tracing the path

Class 06 Project Tracing the path

Instructions : 

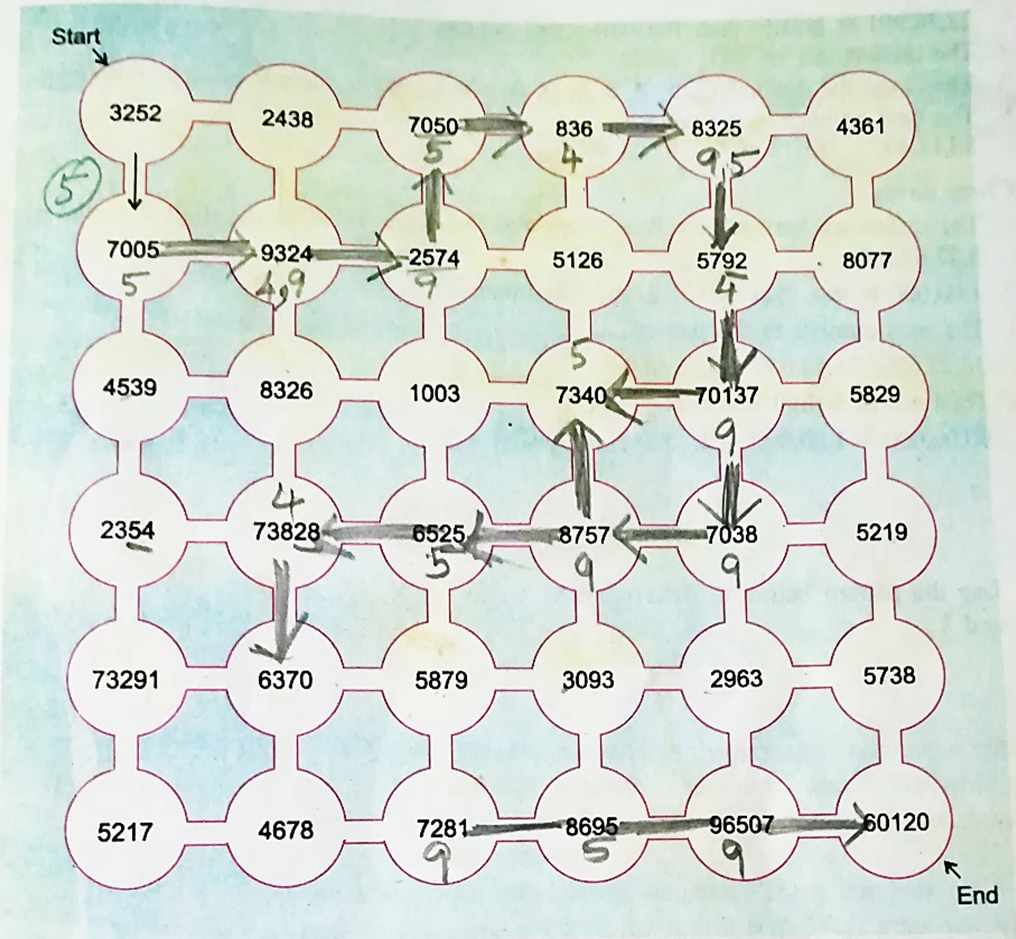
You have to find a path from starting point to the end point, always moving to a circle which is divisible by any one number 4, 5 or 9. 

Procedure:

Starting number is 3252. 

From 3252, you can  move  either to 7005 or 2438. But, 2438 is not divisible by any of the numbers 4, 5 or 9.

However, 7005 is divisible by 5, so, we move to 7005.

2. From 7005 the  two options are  9324 and 4539. But, 9324 is divisible, by both 4 and 9 and 4539 is not divisible by any one of the numbers 4, 5 and 9. so we move to 9324.  

3. Go on to reach the end point.

4. Do you find more than one path?

PROJECT 2 – TRACING THE PATH -Solution

Procedure: 3252 is divisible by 4.

1. 7005 is divisible by 5.

2. 9324 is divisible, by both 4 and 9

3. 9324 is divisible by 4 & 9. 

4. 2574 is divisible by 9.

5. 7050 is divisible by 5.

6. 836 is divisible by 4.

7. 8325 is divisible by 9 & 5.

8. 5792 is divisible by 4.

9. 70137 is divisible by 9.

10. 7340 is divisible by 5.

11. 7038 is divisible by 9.

12. 8757 is divisible by 9.

13. 8525 is divisible by 5.

14. 73828 is divisible by 4.

15. 6370 is divisible by 5

16. 4670 is divisible by 5.

17. 7281 is divisible by 9.

18. 8695 is divisible by 5.

19. 96507 is divisible by 9

20. 60120 is divisible by 5 &9.

reach the end point

Do you find more than one path? Yes.

Class 06 PROJECT MAGIC SQUARE

 Class 06

PROJECT 1- MAGIC SQUARE

Objective :

 To study the principles and formation of magic squares.

Description : 

A magic square is a square array of numbers 1,2,3,4,5….n arranged in such a way that the sum of each row, each column and both diagonals is constant.

Procedure : 

let us develop a magic square.

 Example 1

STEP 1 : Choose any number to start to fill the magic square.

STEP 2 :Let us start from 1 to 16 numbers to fill the square.

STEP 3: All the numbers 1,2,3,4,5,6,7,8,……..16 are written in order from left to right across each row in turn starting from the top left hand corner.

 STEP 4:  Numbers are then interchanged diagonally by opposite numbers. 

PROJECT 1 – KNOWING OUR NUMBERS

Example 2

STEP 1 : Here we choose the numbers from 5 to 20 and make a magic square.

STEP 2 : Fill all the numbers starting from 5, 6, 7, 8 --- 20 in order from left to right across each row in turn, starting from the top left hand corner. (Figure 3).

STEP 3 : Numbers are then interchanged diagonally by opposite numbers.

STEP 4 : We get a magic square of sum of numbers in each row, each column and each diagonal is 50. 

Cup Method

STEP 1 : Write all the 16 numbers from 1 to 16 as shown in figure which seem to be in two cups.

STEP 2 : Number 1 to 8 are written in an open cup and 9 to 16 are written in an inverted cup.

PROJECT 1 – KNOWING OUR NUMBERS

STEP 3 : Now invert the middle rows as shown in the figure.

STEP 4 : The sum of numbers in each row, each column and each diagonal is 34.

STEP 5 :  We can also observe some more interesting facts in this magic square.

(i) The sum of central square is also 34.

(ii) The sum of corner elements of square is also 34.

You can make your own magic squares the same way.

 

Class 06 To find the LCM of two given numbers by using number grid

 Class 06 

To find the LCM of two given numbers by using number grid

ACTIVITY 2 – PLAYING WITH NUMBERS

Objective: 

To find the LCM of two given numbers by using number grid. 

Materials Required: 

geometry box , Squared paper, tracing paper, cardboard sheets, colour pencils, , etc.

Procedure: 

Let us find the LCM of 12 and 18.

STEP 1: Take a 10 x 10 squared paper and write numbers from 1 to 100. Paste the number grid on a cardboard sheet.

STEP 2 : Put a tracing paper over the number grid and trace its boundary. Cut the tracing paper along the boundary drawn to get a square piece exactly of the same size as the number grid.

ACTIVITY 2 – PLAYING WITH NUMBERS

STEP 3:  Repeat the step 2 to get another square piece of tracing paper.

STEP 4: Now find the multiples of 12, which are 12, 24, 36, 48, 60, 72, 84, 96, ......

STEP 5 : Place one of the square pieces on the number grid and colour the squares which contain multiples of 12. 

Mark 1 on the tracing paper to identify the correct position of the tracing paper.

STEP 6: Remove the tracing paper.

ACTIVITY 2 – PLAYING WITH NUMBERS

STEP 7: Find the multiples of 18, which are 18, 36, 54, 72, 90, ......

STEP 8: Place another square piece on the number grid and encircle the multiples of 18 on the tracing paper. Mark 1 on the tracing paper to identify the correct position of the tracing paper.

STEP 9:  Remove the tracing paper.

ACTIVITY 2 – PLAYING WITH NUMBERS

STEP 10: Now place both the square pieces (figures 3 and 5) on the number grid (figure 1), such that these square pieces cover the 

number grid exactly,

Observations:

In STEP 5 , the shaded numbers are multiples of 12.

In STEP 8, the encircled numbers are multiples of 18.

In STEP 10, the numbers which are shaded and encircled are the common multiples of 12and 18, i.e., 36 and 72 common multiples of 12 and 18.

Now 36 is smaller than 72. Hence, LCM (lowest common multiple) of 12 and 18

Conclusion: 

From the above activity, we find that the LCM of 12 and 18 is 36.

Do Yourself: 

By activity method, find the LCM of:

1. 8 and 12 2. 3, 5 and 10 3. 2, 4 and 10 4. 4, 6 and 9

Class 06 To find the HCF of two given numbers by paper cutting and pasting

CLASS 6MATHEMATICS ACTIVITIES

ACTIVITY 1 – PLAYING WITH NUMBERS

Objective: 

To find the HCF of two given numbers by paper cutting and pasting.

Materials Required: 

Coloured chart paper, geometry box, a pair of scissors, cardboard sheet, glue stick, etc.

Procedure: 

Let us find the HCF of 25 and 40.

STEP 1 : From the red chart paper, cut out a strip of length 40 cm and width 1 cm.

STEP 2: From the black chart paper, cut out a strip of length 25 cm and width 1 cm.

STEP 3 : Paste these two strips on a cardboard sheet and cut out both, the red and black portions from the cardboard.

STEP 4: Now, put the smaller strip (black) below the longer strip (red). Cut out the remaining portion of the red strip as shown below. The length of the cut out is 15 cm.

STEP 5 : Now, put the black strip (25 cm long) and the red strip (15 cm long) one below the other. Cut out the remaining portion of the black strip. Its length is 10 cm.

STEP 6 : Now, put the red strip (15 cm long) and the black strip (10 cm long) one below the other Cut out the remaining portion of the red strip. It measures 5 cm.

STEP 7 : Now, put the black strip (10 cm long) and the red strip (5 cm long) one below the other. On keeping the red strip twice, the length of the black strip is completely covered.

Observations:

Finding the HCF of 25 and 40 means we want to find the greatest length which canmeasure 25 cm and 40 cm exactly.

 STEP 4 shows   25) 40 (1

                  - 25

                   15

i.e., the length of the red cut out is 15 cm.

ACTIVITY 1- PLAYING WITH NUMBERS

3. STEP 5 shows  15) 25 (1 

                     -15

                      10

i.e., the length of the black cut out is 10 cm.

4. STEP 6 shows  10 ) 15 (1

                     - 10

                         5

i.e., the length of the red cut out is 5 cm.

5. STEP 7  shows  5 ) 10 ( 2

                    -10

                       0

i.e., the red cut out measures the black strip twice exactly.

6. Thus, we see that the 5 cm long cut out measures 25 cm and 40 cm exactly. 

Hence, HCF of 25 and 40 is 5.

Conclusion: 

From the above activity, we find that the HCF of 25 and 40 is 5.

Do Yourself: 

Find the HCF of the following numbers by the activity method.

8 and 14 2. 15 and 24  3. 16 and 40

4. 9 and 25 5. 30 and 55 6. 45 and 54