Class 06 To make a protractor

 ACTIVITY- Basic Geometrical Ideas

Objective: 

To make a protractor,

Materials Required: 

Some sheets of paper, scissors, geometry box, pencil, etc.

Procedure:

Draw a large semi-circle on a sheet of paper and cut it out. Mark 0 ° and 180 ° at the endpoints of its diameter.

2. Fold it to get a shape as shown alongside.

3. Open out the resulting shape to get a semicircle having a crease line in the middle.

Mark 90 ° on this crease line.

4. Fold the semi-circle twice to get a shape as shown below.

ACTIVITY- Basic Geometrical Ideas

5. Open out the resulting shape. You will get two more crease lines. 

Write 45 ° on the first crease line to the right of 90 ° line and 

(90 ° + 45 °)= 135 ° on the second crease line to the left of 90 ° line. 

6. Fold the semi-circular paper thrice to get a shape as shown below:

Class 06 ACTIVITY – UNDERSTANDING ELEMENTARY SHAPES

 ACTIVITY – UNDERSTANDING ELEMENTARY SHAPES

Objective: 

To illustrate the basic geometrical shapes with set-squares.

Materials Required : 

Chart paper, geometry box, Five set -squares (30 ° -60 °-90 °), 

five set-squares (45 °-45 °-90 °), ruler, pencil

To make a rectangle with the help of two set-squares (30 ° -60 °-90 °)

Procedure:

Take two set-squares (30 ° -60 °-90 °) as shown in Fig. 1.

Place the two set-squares as shown in Fig. 2. It will produce a figure ' ABCD'.

ACTIVITY – UNDERSTANDING ELEMENTARY SHAPES

3. Measure the sides AB, BC, CD and AD with the help of a ruler as shown in Fig. 3 (i), (ii), (iii) and (iv).

You will find that AB = CD and BC = AD.

4. Similarly, measure AC and BD with the help of a ruler. You will find AC = BD.

ACTIVITY – Understanding Elementary Shapes

II. To make a square waith the help of two set-squares (45 ° -45 °-90 ").

Procedure:

1. Take two set-squares (45 °-45 °-90") as shown in Fig

2. Place the two set-squares as shown in Fig. Name the shape as PQRS.

3. Measures the sides PQ, QR,RS and SP with the help of a ruler as shown in fig.

 you will find that PQ = QR= RS = SP

ACTIVITY – Understanding Elementary Shapes

3. Measures the sides PQ, QR,RS and SP with the help of a ruler as shown in fig.

 you will find that PQ = QR= RS = SP.

4. Similarly, measure PR and QS with the help of a ruler. You will find that PR = QS.

ACTIVITY – Understanding Elementary Shapes

Question 6

III. To make a rhombus with the help of 4 set – squares (30 ° -60 °-90 °).

Procedure : 

Place the 4 set – squares (30 ° -60 °-90 °) as shown in fig. It will produce EFGH.

Measure all the sides EF, FG,GH and EH as shown in fig.

You will find that EF = FG = GH = EH. 

3. Similarly measure EG and FH. You will find that EG ≠ FH.

ACTIVITY- Understanding Elementary Shapes

IV. To make a trapezium with the help of 3 set-squares (30 ° – 60 ° – 90 °).

Procedure:

Take a rectangle made with 2 set-squares and join one set-square at the side of rectangle as shown in Fig. Name the figure produced as ABCD.

2. Measure the sides AB, BC, CD and AD with the help of a ruler. ABCD is the required trapezium.

 

ACTIVITY- Understanding Elementary Shapes

V. To  make a  parallelogram with the help of 2 set-squares (30° -60° - 90 °) 

Procedure:

Place the 2 set -squares (30 ° – 60 ° – 90 °) as shown in fig. Name the figure so obtained as ABCD.

2. Measure the sides AB, BC, CD and AD with the help of a ruler. You will find that, AB = CD and BC = AD  ABCD is the required parallelogram.

Class 06 ACTIVITY – BASIC GEOMETRICAL IDEAS

 ACTIVITY – BASIC GEOMETRICAL IDEAS

Objective: 

On the line segment of length 5 cm on a paper:

(a) to make a perpendicular line from a point on the given time by paper folding,

(b) to make a perpendicular line to the given line from a point outside the line by paper folding. 

(c) To make two intersecting lines by paper folding

(d) to make two parallel lines by paper folding.

Materials Required: 

Tracing papers, colour pencils, geometry box, etc.

(a) to make a perpendicular line from a point on the given time by paper folding,

On a tracing paper, draw a line segment AB = 5 cm. Mark a point P on AB

2. Fold the tracing paper at P such that PB falls along PA.

3. Unfold the tracing paper and draw a line XY along the crease, which passes through P. ∟APX = 90°

(b) to make a perpendicular line to the given line from a point outside the line by paper folding. 

4. On a tracing paper, draw a line segment AB = 5 cm.

Mark a point O above or below the line segment AB.

5.Fold the tracing paper such that the folding line passes through O and the two parts of AB coincide.

6.Unfold the tracing paper and draw a line along the crease, which passes through O. ∟OPA = 90°

(c) To make two intersecting lines by paper folding

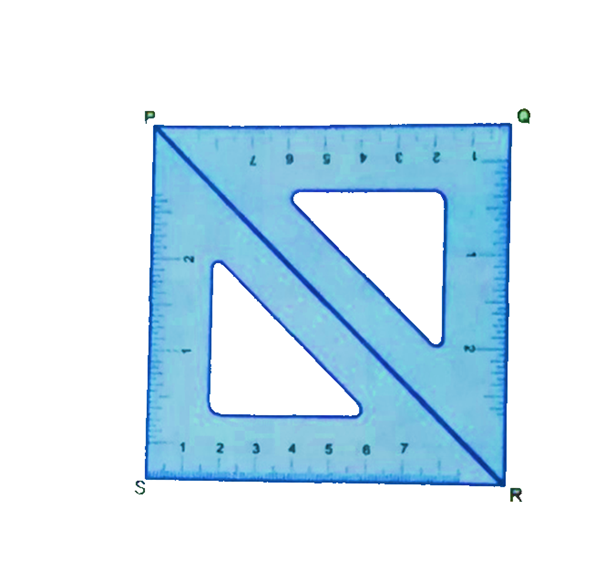
7. Take a sheet of tracing paper PQRS of dimensions 15 cm x 15 cm. In the middle of it draw a line segment AB = 5 cm.

8. Fold the tracing paper, such that SR and RQ coincide.

9. Unfold the tracing paper and draw a line along the crease. 

10. Fold the tracing paper such that RS and SP coincide.

11. Unfold the tracing paper and draw a line along the crease.

(d) To make two parallel lines by paper folding.

12. Take a sheet of tracing paper PQRS. On it draw a line segment AB = 5 cm.

13. Fold the tracing paper such that the folding line falls along AB.

14. Again fold the tracing paper such that AB (first folding line)falls along PQ

15. Unfold the tracing paper and draw lines along the creases. 

Observations: 

On measuring ∠APX, in figure 3, we find that it measures 90 °. Hence, XY is a line perpendicular to AB and passing through P.

2. On measuring ∠OPA, in figure 6, we find that it measures 90 °. Hence, OP is a line perpendicular to AB and passing through O.

3. In figure 11, lines PR and SQ intersect at O. Also, the point of intersection of AB and PR is L and the point of intersection of AB and SQ is M.

4. In figure 15, if we extend each of the lines XY, AB and LM, no two lines intersect. It means XY, AB and LM are parallel lines.

Class 06 To solve a linear equation in one variable

 MATHS ACTIVITIES

CLASS 6

Based on CHAPTERs

11. ALGEBRA

12. Ratio and proportion

4.basic geometrical ideas

5.understanding elementary shapes

ACTIVITY - ALGEBRA

Objective : 

To solve a linear equation in one variable.

Materials Required : 

Balance, some marbles of same weight.

Procedure:  

Let us solve 2x +4 =10

Consider that x represents a bag containing some marbles. The other numbers 4 and 10 are also represented by marbles. The above equation can be represented by the following balance. On the left pan, there are two bags each containing the same (but unknown) number of marbles and four loose marbles. On the right hand pan, there are 10 marbles.

2. Now remove 4 marbles from both sides till you reduce to only one type of shape on either side of the balance.

ACTIVITY - ALGEBRA

3. Now compare items on left and right hand pans.

4. Check what is left with you on each pan of the balance.

We have 2 bags = 6 marbles.

Clearly 2 bags have equal number of marbles and both have total 6 marbles,

Therefore, each bag must contain 3 marbles.

Hence, x = 3 is the solution of the equation.

Do Yourself ; 

Solve the following linear equations by activity method :

(i) 3x+3= 12 

(ii) 2x + 5=9