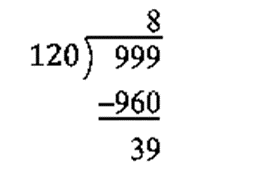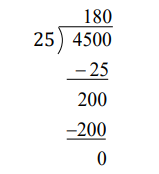Sunday, December 17, 2023

Class – 6 CH-3 PLAYING WITH NUMBERS MATHS NCERT SOLUTIONS

Class – 6 CH-3 PLAYING WITH NUMBERS

MATHS NCERT SOLUTIONS

Exercise 3.1

Question 1:

Write all the factors of the following numbers:

(a) 24 (b) 15 (c) 21 (d)27

(e) 12 (f) 20 (g) 18 (h) 23 (i) 36

Solution 1:

(a) 24 = 1 x 24 = 2 x 12 = 3 x 8 = 4 x 6 = 6 x 4

Factors of 24 = 1, 2, 3, 4, 6, 12, 24

(b) 15 = 1 x 15 = 3 x 5 = 5 x 3

Factors of 15 = 1, 3, 5, 15

Factors of 21 = 1, 3, 7, 21

(d) 27 = 1 x 27 = 3 x 9 = 9 x 3

Factors of 27 = 1, 3, 9, 27

(e) 12 = 1 x 12 = 2 x 6 = 3 x 4 = 4 x 3

Factors of 12 = 1, 2, 3, 4, 6, 12

(f) 20 = 1 x 20 = 2 x 10 = 4 x 5 = 5 x 4

Factors of 20 = 1, 2, 4, 5, 10, 20

(g) 18 = 1 x 18 = 2 x 9 = 3 x 6

Factors of 18 = 1, 2, 3, 6, 9, 18

(h) 23 = 1 x 23

Factors of 23 = 1, 23

(i) 36 = 1 x 36 = 2 x 18 = 3 x 12 = 4 x 9 = 6 x 6

Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36

Question 2:

Write first five multiples of:

(a) 5 (b) 8 (c) 9 (d) 27

Solution 2:

(a) 5 x 1 = 5, 5 x 2 = 10, 5 x 3 = 15, 5 x 4 = 20, 5 x 5 =25

First five multiples of 5 are 5, 10, 15, 20, 25.

(b) 8 x 1 = 8, 8 x 2 = 16, 8 x 3 = 24, 8 x 4 = 32, 8 x 5 = 40

First five multiples of 8 are 8, 16, 24, 32, 40.

First five multiples of 9 are 9, 18, 27, 36, 45.

Question 3:

Match the items in column 1 with the items in column 2:

Column 1 Column 2

(i) 35 (a) Multiple of 8

(ii) 15 (b) Multiple of 7

(iii) 16 (c) Multiple of 70

(iv) 20 (d) Factor of 30

(v) 20 (e) Factor of 50

Solution 3:

(i) - (b)

(ii) - (d)

(iii) - (a)

(iv) - (f)

(v) - (e)

Question 4:

Find all the multiples of 9 up to 100.

Solution 4:

Multiples of 9 up to 100 are: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99

Exercise 3.2

Question 1:

What is the sum of any two:

(a) Odd numbers.

(b) Even numbers.

Solution 1:

(a) The sum of any two odd numbers is an even number.

Example: 1 + 3 = 4, 3 + 5 = 8

(b) The sum of any two even numbers is also an even number.

Example: 2 + 4 = 6, 6 + 8 = 14

Question 2:

State whether the following statements are true or false: (a) The sum of three odd numbers is even.

(b) The sum of two odd numbers and one even number is even.

(d) If an even number is divided by 2, the quotient is always odd.

(e) All prime numbers are odd.

(f) Prime numbers do not have any factors.

(g) Sum of two prime numbers is always even.

(h) 2 is the only even prime number.

(i) All even numbers are composite numbers.

(j) The product of two even numbers is always even.

Solution 2:

(a) False

(b) True

(d) False

(e) False

(f) False

(g) False

(h) True

(i) False

(j) True

Question 3:

The numbers 13 and 31 are prime numbers. Both these numbers have same digits 1 and 3. Find such pairs of prime numbers up to 100.

Solution 3:

17 and 71; 37 and 73; 79 and 97

Question 4:

Write down separately the prime and composite numbers less than 20.

Solution 4:

Prime numbers : 2, 3, 5, 7, 11, 13, 17, 19

Composite numbers : 4, 6, 8, 9, 10, 12, 14, 15, 16, 18

Question 5:

What is the greatest prime number between 1 and 10?

Solution 5:

The greatest prime number between 1 and 10 is ‘7’.

Question 6:

Express the following as the sum of two odd numbers:

(a) 44 (b) 36 (c) 24 (d) 18

Solution 6:

(a) 3 + 41 = 44

(b) 5 + 31 = 36

(d) 7 + 11 = 18

Question 7:

Give three pairs of prime numbers whose difference is 2.

[Remark: Two prime numbers whose difference is 2 are called twin primes.]

Solution 7:

3 and 5; 5 and 7; 11 and 13

Question 8:

Which of the following numbers are prime:

(a) 23 (b) 51 (c) 37 (d) 26

Solution 8:

(a) 23 and (c) 37 are prime numbers.

Question 9:

Write seven consecutive composite numbers less than 100 so that there is no prime number between them.

Solution 9:

Seven consecutive composite numbers: 90, 91, 92, 93, 94, 95, 96

Question 10:

Express each of the following numbers as the sum of three odd primes:

(a) 21 (b) 31 (c) 53 (d) 61

Solution 10:

(a) 21 = 3 + 7 + 11

(b) 31 = 3 + 11 + 17

(d) 61 = 19 + 29 + 13

Question 11:

Write five pairs of prime numbers less than 20 whose sum is divisible by 5.

[Hint: 3 + 7 = 10]

Solution 11:

2+ 3 = 5;

7 + 13 = 20;

3+ 17 = 20;

2 + 13 = 15;

5 + 5 = 10

Question 12:

Fill in the blanks:

(a) A number which has only two factors is called a _______________.

(b) A number which has more than two factors is called a _______________.

(d) The smallest prime number is _______________.

(e) The smallest composite number is _______________.

(f) The smallest even number is _______________.

Solution 12:

(a) Prime number

(b) Composite number

(d) 2

(e) 4

(f) 2

Exercise 3.3

Question 1:

Using divisibility test, determine which of the following numbers are divisible by 2; by 3; by 4; by 5; by 6; by 8; by 9; by 10; by 11. (Say yes or no)

Number Divisible by

2 3 4 5 6 8 9 10 11

128

990

1586

275

6686

639210

429714

2856

3060

406839 Yes No Yes No No Yes No No No

Solution 1:

Number Divisible by

Question 2:

Using divisibility test, determine which of the following numbers are divisibly by 4; by 8:

(a) 572 (b) 726352 (c) 5500 (d) 6000

(e) 12159 (f) 14560 (g) 21084 (h) 31795072

(i) 1700 (j) 2150

Solution 2:

(a) 572 - Divisible by 4 as its last two digits are divisible by 4.

Not divisible by 8 as its last three digits are not divisible by 8.

(b) 726352 - Divisible by 4 as its last two digits are divisible by 4.

Divisible by 8 as its last three digits are divisible by 8.

 Not divisible by 8 as its last three digits are not divisible by 8.

(d) 6000 Divisible by 4 as its last two digits are 0.

Divisible by 8 as its last three digits are 0.

(e) 12159 Not divisible by 4 and 8 as it is an odd number.

(f) 14560 Divisible by 4 as its last two digits are divisible by 4.

Divisible by 8 as its last three digits are divisible by 8.

(g) 21084 Divisible by 4 as its last two digits are divisible by 4.

Not divisible by 8 as its last three digits are not divisible by 8.

(h) 31795072 Divisible by 4 as its last two digits are divisible by 4.

Divisible by 8 as its last three digits are divisible by 8.

(i) 1700 Divisible by 4 as its last two digits are 0.

Not divisible by 8 as its last three digits are not divisible by 8.

(j) 5500 Not divisible by 4 as its last two digits are not divisible by 4.

Not divisible by 8 as its last three digits are not divisible by 8.

Question 3:

Using divisibility test, determine which of the following numbers are divisible by 6:

(a) 297144 (b) 1258 (c) 4335 (d) 61233

(e) 901352 (f) 438750 (g) 1790184 (h) 12583

(i) 639210 (j) 17852

Solution 3:

(a) 297144 - Divisible by 2 as its units place is an even number.

- Divisible by 3 as sum of its digits (= 27) is divisible by 3.

Since the number is divisible by both 2 and 3, therefore, it is also divisible by 6.

(b) 1258 - Divisible by 2 as its units place is an even number.

- Not divisible by 3 as sum of its digits (= 16) is not divisible by 3. Since the number is not divisible by both 2 and 3, therefore, it is not divisible by 6.

- Divisible by 3 as sum of its digits (= 15) is divisible by 3.

Since the number is not divisible by both 2 and 3, therefore, it is not divisible by 6.

(d) 61233 - Not divisible by 2 as its units place is not an even number.

- Divisible by 3 as sum of its digits (= 15) is divisible by 3.

Since the number is not divisible by both 2 and 3, therefore, it is not divisible by 6.

(e) 901352 - Divisible by 2 as its units place is an even number.

- Not divisible by 3 as sum of its digits (= 20) is not divisible by 3. Since the number is not divisible by both 2 and 3, therefore, it is not divisible by 6.

(f) 438750 - Divisible by 2 as its units place is an even number.

Divisible by 3 as sum of its digits (= 27) is not divisible by 3. Since the number is divisible by both 2 and 3, therefore, it is divisible by 6.

(g) 1790184 - Divisible by 2 as its units place is an even number.

- Divisible by 3 as sum of its digits (= 30) is not divisible by 3. Since the number is divisible by both 2 and 3, therefore, it is divisible by 6.

(h) 12583 - Not divisible by 2 as its units place is not an even number.

- Not divisible by 3 as sum of its digits (= 19) is not divisible by 3. Since the number is not divisible by both 2 and 3, therefore, it is not divisible by 6. (i) 639210  Divisible by 2 as its units place is an even number.

- Divisible by 3 as sum of its digits (= 21) is not divisible by 3. Since the number is divisible by both 2 and 3, therefore, it is divisible by 6.

(j) 17852 - Divisible by 2 as its units place is an even number.

 Not divisible by 3 as sum of its digits (= 23) is not divisible by 3. Since the number is not divisible by both 2 and 3, therefore, it is not divisible by 6.

Question 4:

Using divisibility test, determine which of the following numbers are divisible by 11:

(a) 5445 (b) 10824 (c) 7138965 (d) 70169308

(e) 10000001 (f) 901153

Solution 4:

(a) 5445 - Sum of the digits at odd places = 4 + 5 = 9

Sum of the digits at even places = 4 + 5 = 9

Difference of both sums = 9 – 9 = 0

Since the difference is 0, therefore, the number is divisible by 11.

(b) 10824 - Sum of the digits at odd places = 4 + 8 +1 = 13

Sum of the digits at even places = 2 + 0 = 2

Difference of both sums = 13 – 2 = 11

Since the difference is 11, therefore, the number is divisible by 11.

 Sum of the digits at even places = 6 + 8 + 1 = 15

 Difference of both sums = 24 – 15 = 9

Since the difference is neither 0 nor 11, therefore, the number is not divisible by 11.

(d) 70169308- Sum of the digits at odd places = 8 + 3 + 6 + 0 = 17

 Sum of the digits at even places = 0 + 9 + 1 + 7 = 17

 Difference of both sums = 17 – 17 = 0

Since the difference is 0, therefore, the number is divisible by 11.

(e) 10000001 - Sum of the digits at odd places = 1 + 0 + 0 + 0 = 1

 Sum of the digits at even places = 0 + 0 + 0 + 1 = 1

 Difference of both sums = 1 – 1 = 0

Since the difference is 0, therefore, the number is divisible by 11.

(f) 901153 - Sum of the digits at odd places = 3 + 1 + 0 = 4

 Sum of the digits at even places = 5 + 1 + 9 = 15

 Difference of both sums = 15 – 4 = 11

Since the difference is 11, therefore, the number is divisible by 11.

Question 5:

Write the smallest digit and the largest digit in the blanks space of each of the following numbers so that the number formed is divisibly by 3:

(a) __________ 6724 (b) 4765 __________ 2

Solution 5:

(a) We know that a number is divisible by 3 if the sum of all digits is divisible by 3. Therefore, Smallest digit : 2  26724 = 2 + 6 + 7 + 2 + 4 = 21

Largest digit : 8  86724 = 8 + 6 + 7 + 2 + 4 = 27

(b) We know that a number is divisible by 3 if the sum of all digits is divisible by 3. Therefore, Smallest digit : 0  476502 = 4 + 7 + 6 + 5 + 0 + 2 = 24

Largest digit : 9  476592 = 4 + 7 + 6 + 5 + 0 + 2 = 33

Question 6:

Write the smallest digit and the largest digit in the blanks space of each of the following numbers so that the number formed is divisibly by 11:

(a) 92 __________ 389 (b) 8 __________ 9484

Solution 6:

(a) We know that a number is divisible by 11 if the difference of the sum of the digits at odd places and that of even places should be either 0 or 11.

Therefore, 928389  Odd places = 9 + 8 + 8 = 25

Even places = 2 + 3 + 9 = 14

Difference = 25 – 14 = 11

(b) We know that a number is divisible by 11 if the difference of the sum of the digits at odd places and that of even places should be either 0 or 11.

Therefore, 869484  Odd places = 8 + 9 + 8 = 25

Even places = 6 + 4 + 4 = 14

Difference = 25 – 14 = 11

Exercise 3.4

Question 1:

Find the common factors of:

(a) 20 and 28 (b) 15 and 25

Solution 1:

(a) Factors of 20 = 1, 2, 4, 5, 10, 20

Factors of 28 = 1, 2, 4, 7, 14, 28

Common factors = 1, 2, 4

(b) Factors of 15 = 1, 3, 5, 15 Factors of 25 = 1, 5, 25

Common factors = 1, 5

Factors of 50 = 1, 2, 5, 10, 25, 50

Common factors = 1, 5

(d) Factors of 56 = 1, 2, 4, 7, 8, 14, 28, 56

Factors of 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 60, 120

Common factors = 1, 2, 4, 8

Question 2:

Find the common factors of:

(a) 4, 8 and 12 (b) 5, 15 and 25

Solution 2:

(a) Factors of 4 = 1, 2, 4

Factors of 8 = 1, 2, 4, 8

Factors of 12 = 1, 2, 3, 4, 6, 12

Common factors of 4, 8 and 12 = 1, 2, 4

(b) Factors of 5 = 1, 5

Factors of 15 = 1, 3, 5, 15

Factors of 25 = 1, 5, 25

Common factors of 5, 15 and 25 = 1, 5

Question 3:

Find the first three common multiples of:

(a) 6 and 8 (b) 12 and 18

Solution 3:

(a) Multiple of 6 = 6, 12, 18, 24, 30, 36, 42, 28, 54, 60, 72, …………

Multiple of 8 = 8, 16, 24, 32, 40, 48, 56, 64, 72, …………………….

Common multiples of 6 and 8 = 24, 48, 72

(b) Multiple of 12 = 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, ………

Multiple of 18 = 18, 36, 54, 72, 90, 108, ………………………………

Common multiples of 12 and 18 = 36, 72, 108

Question 4:

Write all the numbers less than 100 which are common multiples of 3 and 4.

Solution 4:

Multiple of 3 = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99

Multiple of 4 = 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100

Common multiples of 3 and 4 = 12, 24, 36, 48, 60, 72, 84, 96

Question 5:

Which of the following numbers are co-prime:

(a) 18 and 35 (b) 15 and 37

Solution 5:

(a) Factors of 18 = 1, 2, 3, 6, 9, 18

Factors of 35 = 1, 5, 7, 35

Common factor = 1

Since, both have only one common factor, i.e., 1, therefore, they are co-prime numbers.

(b) Factors of 15 = 1, 3, 5, 15

Factors of 37 = 1, 37

Common factor = 1

Since, both have only one common factor, i.e., 1, therefore, they are co-prime numbers.

Factors of 415 = 1, 5, …….., 83, 415

Common factor = 1, 5

Since, both have more than one common factor, therefore, they are not co-prime numbers.

(d) Factors of 17 = 1, 17

Factors of 68 = 1, 2, 4, 17, 34, 86

Common factor = 1, 17

Since, both have more than one common factor, therefore, they are not co-prime numbers.

(e) Factors of 216 = 1, 2, 3, 4, 6, 8, 36, 72, 108, 216

Factors of 215 = 1, 5, 43, 215

Common factor = 1

Since, both have only one common factor, i.e., 1, therefore, they are co-prime numbers.

(f) Factors of 81 = 1, 3, 9, 27, 81

Factors of 16 = 1, 2, 4, 8, 16

Common factor = 1

Since, both have only one common factor, i.e., 1, therefore, they are co-prime numbers.

Question 6:

A number is divisible by both 5 and 12. By which other number will that number be always divisible?

Solution 6:

5 x 12 = 60. The number must be divisible by 60.

Question 7:

A number is divisible by 12. By what other numbers will that number be divisible?

Solution 7:

Factors of 12 are 1, 2, 3, 4, 6 and 12.

Therefore, the number also be divisible by 1, 2, 3 4 and 6.

Exercise 3.5

Question 1:

Which of the following statements are true:

(a) If a number is divisible by 3, it must be divisible by 9.

(b) If a number is divisible by 9, it must be divisible by 3.

(d) If a number is divisible by 9 and 10 both, then it must be divisible by 90.

(e) If two numbers are co-primes, at least one of them must be prime.

(f) All numbers which are divisible by 4 must also by divisible by 8.

(g) All numbers which are divisible by 8 must also by divisible by 4.

(h) If a number is exactly divides two numbers separately, it must exactly divide their sum.

(i) If a number is exactly divides the sum of two numbers, it must exactly divide the two numbers separately.

Solution 1:

Statements (b), (c), (d), (g) and (h) are true.

Question 2:

Here are two different factor trees for 60. Write the missing numbers. (a)

Solution 2:

Question 3:

Which factors are not included in the prime factorization of a composite number?

Solution 3:

1 is the factor which is not included in the prime factorization of a composite number.

Question 4:

Write the greatest 4-digit number and express it in terms of its prime factors.

Solution 4:

The greatest 4-digit number = 9999

The prime factors of 9999 are 3 × 3 × 11 × 101.

Question 5:

Write the smallest 5-digit number and express it in terms of its prime factors.

Solution 5:

The smallest five digit number is 10000.

The prime factors of 10000 are 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5.

Question 6:

Find all the prime factors of 1729 and arrange them in ascending order. Now state the relation, if any, between, two consecutive prime numbers.

Solution 6:

Prime factors of 1729 are 7 × 13 × 19.

The difference of two consecutive prime factors is 6.

Question 7:

The product of three consecutive numbers is always divisible by 6. Verify this statement with the help of some examples.

Solution 7:

Among the three consecutive numbers, there must be one even number and one multiple of 3. Thus, the product must be multiple of 6.

Example:

(i) 2 x 3 x 4 = 24

(ii) 4 x 5 x 6 = 120

Question 8:

The sum of two consecutive odd numbers is always divisible by 4. Verify this statement with the help of some examples.

Solution 8:

3 + 5 = 8 and 8 is divisible by 4.

5 + 7 = 12 and 12 is divisible by 4.

7 + 9 = 16 and 16 is divisible by 4.

9 + 11 = 20 and 20 is divisible by 4.

Question 9:

In which of the following expressions, prime factorization has been done:

(a) 24 = 2 x 3 x 4

(b) 56 = 7 x 2 x 2 x 2

(d) 54 = 2 x 3 x 9

Solution 9:

In expressions (b) and (c), prime factorization has been done.

Question 10:

Determine if 25110 is divisible by 45.

[Hint: 5 and 9 are co-prime numbers. Test the divisibility of the number by 5 and 9.]

Solution 10:

The prime factorization of 45 = 5 x 9

25110 is divisible by 5 as ‘0’ is at its unit place.

25110 is divisible by 9 as sum of digits is divisible by 9.

Therefore, the number must be divisible by 5 x 9 = 45

Question 11:

18 is divisible by both 2 and 3. It is also divisible by 2 x 3 = 6.

Similarly, a number is divisible by 4 and 6.

Can we say that the number must be divisible by 4 x 6 = 24? If not, give an example to justify your Solution.

Solution 11:

No. Number 12 is divisible by both 6 and 4 but 12 is not divisible by 24.

Question 12:

I am the smallest number, having four different prime factors. Can you find me?

Solution 12:

The smallest four prime numbers are 2, 3, 5 and 7.

Hence, the required number is 2 x 3 x 5 x 7 = 210

Exercise 3.6

Question 1:

Find the H.C.F. of the following numbers:

(a) 18, 48

(b) 30, 42

(d) 27, 63

(e) 36, 84

(f) 34, 102

(g) 70, 105, 175

(h) 91, 112, 49

(i) 18, 54, 81

(j) 12, 45, 75

Solution 1:

(a) Factors of 18 = 2 x 3 x 3

Factors of 48 = 2 x 2 x 2 x 2 x 3

H.C.F. (18, 48) = 2 x 3 = 6

(b) Factors of 30 = 2 x 3 x 5

Factors of 42 = 2 x 3 x 7

H.C.F. (30, 42) = 2 x 3 = 6

Factors of 60 = 2 x 2 x 3 x 5

H.C.F. (18, 60) = 2 x 3 = 6

(d) Factors of 27 = 3 x 3 x 3

Factors of 63 = 3 x 3 x 7

H.C.F. (27, 63) = 3 x 3 = 9

(e) Factors of 36 = 2 x 2 x 3 x 3

Factors of 84 = 2 x 2 x 3 x 7

H.C.F. (36, 84) = 2 x 2 x 3 = 12

(f) Factors of 34 = 2 x 17

Factors of 102 = 2 x 3 x 17

H.C.F. (34, 102) = 2 x 17 = 34

(g) Factors of 70 = 2 x 5 x 7

Factors of 105 = 3 x 5 x 7

Factors of 175 = 5 x 5 x 7

H.C.F. = 5 x 7 = 35

(h) Factors of 91 = 7 x 13

Factors of 112 = 2 x 2 x 2 x 2 x 7

Factors of 49 = 7 x 7

H.C.F. = 1 x 7 = 7

(i) Factors of 18 = 2 x 3 x 3

Factors of 54 = 2 x 3 x 3 x 3

Factors of 81 = 3 x 3 x 3 x 3

H.C.F. = 3 x 3 = 9

(j) Factors of 12 = 2 x 2 x 3

Factors of 45 = 3 x 3 x 5

Factors of 75 = 3 x 5 x 5

H.C.F. = 1 x 3 = 3

Question 2:

What is the H.C.F. of two consecutive:

(a) numbers?

(b) even numbers?

Solution 2:

(a) H.C.F. of two consecutive numbers be 1.

(b) H.C.F. of two consecutive even numbers be 2.

Question 3:

H.C.F. of co-prime numbers 4 and 15 was found as follows by factorization:

4 = 2 x 2 and 15 = 3 x 5 since there is no common prime factor, so H.C.F. of 4 and 15 is 0. Is the Solution correct? If not, what is the correct H.C.F.?

Solution 3:

No. The correct H.C.F. is 1.

Exercise 3.7

Question 1:

Renu purchases two bags of fertilizer of weights 75 kg and 69 kg. Find the maximum value of weight which can measure the weight of the fertilizer exact number of times.

Solution 1:

For finding maximum weight, we have to find H.C.F. of 75 and 69.

Factors of 75 = 3 x 5 x 5

Factors of 69 = 3 x 69

H.C.F. = 3

Therefore the required weight is 3 kg.

Question 2:

Three boys step off together from the same spot. Their steps measure 63 cm, 70 cm and 77 cm respectively. What is the maximum distance each should cover so that all can cover the distance in complete steps?

Solution 2:

For finding minimum distance, we have to find L.C.M of 63, 70 and 77.

L.C.M. of 63, 70 and 77 = 7 x 9 x 10 x 11 = 6930 cm. Therefore, the minimum distance is 6930 cm.

Question 3:

The length, breadth and height of a room are 825 cm, 675 cm and 450 cm respectively. Find the longest tape which can measure the three dimensions of the room exactly.

Solution 3:

The measurement of longest tape = H.C.F. of 825 cm, 675 cm and 450 cm.

Factors of 825 = 3 x 5 x 5 x 11

Factors of 675 = 3 x 5 x 5 x 3 x 3

Factors of 450 = 2 x 3 x 3 x 5 x 5

H.C.F. = 3 x 5 x 5 = 75 cm

Therefore, the longest tape is 75 cm.

Question 4:

Determine the smallest 3-digit number which is exactly divisible by 6, 8 and 12.

Solution 4:

L.C.M. of 6, 8 and 12 = 2 x 2 x 2 x 3 = 24

The smallest 3-digit number = 100

To find the number, we have to divide 100 by 24

100 = 24 x 4 + 4

Therefore, the required number = 100 + (24 – 4) = 120.

Question 5:

Determine the largest 3-digit number which is exactly divisible by 8, 10 and 12.

Solution 5:

L.C.M. of 8, 10, 12 = 2 x 2 x 2 x 3 x 5 = 120

The largest three digit number = 999

Now,

Therefore, the required number = 999 – 39 = 960

Question 6:

The traffic lights at three different road crossings change after every 48 seconds, 72 seconds and 108 seconds respectively. If they change simultaneously at 7 a.m. at what time will they change simultaneously again?

Solution 6:

L.C.M. of 48, 72, 108 = 2 x 2 x 2 x 2 x 3 x 3 x 3 = 432 sec.

After 432 seconds, the lights change simultaneously.

432 second = 7 minutes 12 seconds

Therefore the time = 7 a.m. + 7 minutes 12 seconds

= 7:07:12 a.m.

Question 7:

Three tankers contain 403 litres and 465 litres of diesel respectively. Find the maximum capacity of a container that can measure the diesel of three containers exact number of times.

Solution 7:

The maximum capacity of container = H.C.F. (403, 434, 465)

Factors of 403 = 13 x 31

Factors of 434 = 2 x 7 x 31

Factors of 465 = 3 x 5 x 31

H.C.F. = 31

Therefore, 31 litres of container is required to measure the quantity.

Question 8:

Find the least number which when divided by 6, 15 and 18, leave remainder 5 in each case.

Solution 8:

L.C.M. of 6, 15 and 18 = 2 x 3 x 3 x 5 = 90

Therefore, the required number = 90 + 5 = 95

Question 9:

Find the smallest 4-digit number which is divisible by 18, 24 and 32.

Solution 9:

L.C.M. of 18, 24 and 32 = 2 x 2 x 2 x 2 x 2 x 3 x 3 = 288

The smallest four-digit number = 1000

Therefore, the required number is 1000 + (288 – 136) = 1152.

Question 10:

Find the L.C.M. of the following numbers:

(a) 9 and 4 (b) 12 and 5 (c) 6 and 5 (d) 15 and 4

Observe a common property in the obtained L.C.Ms. Is L.C.M. the product of two numbers in each case?

Solution 10:

(a) L.C.M. of 9 and 4

LCM= 2 x 2 x 3 x 3

= 36

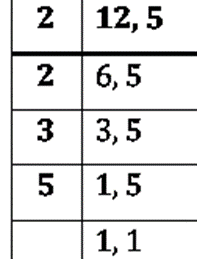
(b) L.C.M. of 12 and 5

= 2 x 2 x 3 x 5

= 60

= 2 x 3 x 5

= 30

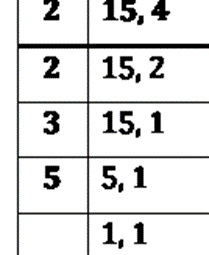
(d) L.C.M. of 15 and 4

= 2 x 2 x 3 x 5

= 60

Yes, the L.C.M. is equal to the product of two numbers in each case. And L.C.M. is also the multiple of 3.

Question 11:

Find the L.C.M. of the following numbers in which one number is the factor of other:

(a) 5, 20 (b) 6, 18 (c) 12, 48 (d) 9, 45

What do you observe in the result obtained?

Solution 11:

(a) L.C.M. of 5 and 20

LCM= 2 x 2 x 5

= 20

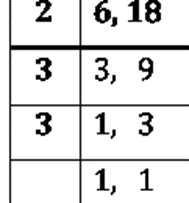
(b) L.C.M. of 6 and 18

LCM = 2 x 3 x 3

= 18

LCM= 2 x 2 x 2 x 2 x 3 = 48

(d) L.C.M. of 9 and 45

LCM= 3 x 3 x 5

= 45

From these all cases, we can conclude that if the smallest number if the factor of largest number, then the L.C.M. of these two numbers is equal to that of larger number.

Class – 6 CH-2 WHOLE NUMBERS MATHS NCERT SOLUTIONS

Class – 6 CH-2 WHOLE NUMBERS

NCERT SOLUTIONS

Exercise 2.1

Question 1:

Write the next three natural numbers after 10999.

SOLUTION 1:

10,999 + 1 = 11,000

11,000 + 1 = 11,001

11,001 + 1 = 11,002

Question 2:

Write the three whole numbers occurring just before 10001.

SOLUTION 2:

10,001 – 1 = 10,000

10,000 – 1 = 9,999

9,999 – 1 = 9,998

Question 3:

Which is the smallest whole number?

SOLUTION 3:

‘0’ (zero) is the smallest whole number.

Question 4:

How many whole numbers are there between 32 and 53?

SOLUTION 4:

53 – 32 – 1 = 20

There are 20 whole numbers between 32 and 53.

Question 5:

Write the successor of:

(a) 2440701

(b) 100199

(d) 2345670

SOLUTION 5:

(a) Successor of 2440701 is 2440701 + 1 = 2440702

(b) Successor of 100199 is 100199 + 1 = 100200

(d) Successor of 2345670 is 2345670 + 1 = 2345671

Question 6:

Write the predecessor of:

(a) 94

(b) 10000

(d) 7654321

SOLUTION 6:

(a) The predecessor of 94 is 94 – 1 = 93

(b) The predecessor of 10000 is 10000 – 1 = 9999

(d) The predecessor of 7654321 is 7654321 – 1 = 7654320

Question 7:

In each of the following pairs of numbers, state which whole number is on the left of the other number on the number line? Also write them with the appropriate sign (>, <) between them.

(a) 530, 503

(b) 370, 307

(d) 9830415, 10023001

SOLUTION 7:

(a) 530 > 503;

So 503 appear on left side of 530 on number line.

(b) 370 > 307;

So 307 appear on left side of 370 on number line.

So 56789 appear on left side of 98765 on number line.

(d) 9830415 < 10023001;

So 9830415 appear on left side of 10023001 on number line.

Question 8:

Which of the following statements are true (T) and which are false (F):

(a) Zero is the smallest natural number.

(b) 400 is the predecessor of 399.

(d) 600 is the successor of 599.

(e) All natural numbers are whole numbers.

(f) All whole numbers are natural numbers.

(g) The predecessor of a two digit number is never a single digit number.

(h) 1 is the smallest whole number.

(i) The natural number 1 has no predecessor.

(j) The whole number 1 has no predecessor.

(k) The whole number 13 lies between 11 and 12.

(l) The whole number 0 has no predecessor.

(m) The successor of a two digit number is always a two digit number.

SOLUTION 8:

(a) False

(b) False

(d) True

(e) True

(f) False

(g) False

(h) False

(i) True

(j) False

(k) False

(l) True

(m) False

Exercise 2.2

Question 1:

Find the sum by suitable rearrangement:

(a) 837 + 208 + 363

(b) 1962 + 453 + 1538 + 647

SOLUTION 1:

(a) 837 + 208 + 363

= (837 + 363) + 208

= 1200 + 208

= 1408

(b) 1962 + 453 + 1538 + 647

= (1962 + 1538) + (453 + 647)

= 3500 + 1100

= 4600

Question 2:

Find the product by suitable arrangement:

(a) 2 x 1768 x 50

(b) 4 x 166 x 25

(d) 625 x 279 x 16

(e) 285 x 5 x 60

(f) 125 x 40 x 8 x 25

SOLUTION 2:

(a) 2 x 1768 x 50

= (2 x 50) x 1768

= 100 x 1768

= 176800

(b) 4 x 166 x 25

= (4 x 25) x 166

= 100 x 166

= 16600

= (8 x 125) x 291

= 1000 x 291

= 291000

(b) 625 x 279 x 16

= (625 x 16) x 279

= 10000 x 279

= 2790000

(e) 285 x 5 x 60

= 284 x (5 x 60)

= 284 x 300

= 85500

(f) 125 x 40 x 8 x 25

= (125 x 8) x (40 x 25)

= 1000 x 1000

= 1000000

Question 3:

Find the value of the following:

(a) 297 x 17 + 297 x 3

(b) 54279 x 92 + 8 x 54279

(d) 3845 x 5 x 782 + 769 x 25 x 218

SOLUTION 3:

(a) 297 x 17 + 297 x 3

= 297 x (17 + 3)

= 297 x 20

= 5940

(b) 54279 x 92 + 8 x 542379

= 54279 x (92 + 8)

= 54279 x 100

= 5427900

= 81265 x (169 – 69)

= 81265 x 100

= 8126500

(d) 3845 x 5 x 782 + 769 x 25 x 218

= 3845 x 5 x 782 + 3845 x 5 x 218

= 3845 x 5 x (782 + 218)

= 3845 x 5 x 1000

= 19225000

Question 4:

Find the product using suitable properties:

(a) 738 x 103

(b) 854 x 102

(d) 1005 x 168

SOLUTION 4:

(a) 738 x 103

= 738 x (100 + 3)

= 738 x 100 + 738 x 3

= 73800 + 2214

= 76014

(b) 854 x 102

= 854 x (100 + 2)

= 854 x 100 + 854 x 2

= 85400 + 1708

= 87108

= 258 x (1000 + 8)

= 258 x 1000 + 258 x 8

= 258000 + 2064

= 260064

(d) 1005 x 168

= (1000 + 5) x 168

= 1000 x 168 + 5 x 168

= 168000 + 840

= 168840

Question 5:

A taxi-driver, filled his car petrol tank with 40 litres of petrol on Monday. The next day, he filled the tank with 50 litres of petrol. If the petrol costs ₹ 44 per litre, how much did he spend in all on petrol?

SOLUTION 5:

Petrol filled on Monday = 40 litres

Petrol filled on next day = 50 litres

Total petrol filled = 90 litres

Now,

Cost of 1 litre petrol = ₹ 44

Cost of 90 litres petrol = 44 x 90

= 44 x (100 – 10)

= 44 x 100 – 44 x 10

= 4400 – 440

= ₹ 3960

Therefore, he spent ₹ 3960 on petrol.

Question 6:

A vendor supplies 32 litres of milk to a hotel in a morning and 68 litres of milk in the evening. If the milk costs ₹15 per litre, how much money is due to the vendor per day?

SOLUTION 6:

Supply of milk in morning = 32 litres

Supply of milk in evening = 68 litres

Total supply = 32 + 68 = 100 litres

Now

Cost of 1 litre milk = ₹15

Cost of 100 litres milk = 15 x 100 = ₹1500 Therefore, ₹1500 is due to the vendor per day.

Question 7:

Match the following:

(i) 425 x 136 = 425 x (6 + 30 + 100) (a)Commutativity under multiplication

(ii) 2 x 48 x 50 = 2 x 50 x 49 (b) Commutativity under addition

(iii) 80 + 2005 + 20 = 80 + 20 + 2005 (c) Distributivity multiplication under addition

SOLUTION 7:

(i) 425 x 136 = 425 x (6 + 30 + 100) - Distributivity of multiplication over addition

(ii) 2 x 49 x 50 = 2 x 50 x 49 - Commutivity under multiplication

(iii) 80 + 2005 + 20 = 80 + 20 + 2005 - Commutivity under addition

Exercise 2.3

Question 1:

Which of the following will not represent zero:

(a) 1 + 0 (b) 0 x 0 (c) 0/2 (d) 10-10/2

SOLUTION 1:

(a) [1 + 0 is equal to 1]

Question 2:

If the product of two whole numbers is zero, can we say that one or both of them will be zero? Justify through examples.

SOLUTION 2:

Yes, if we multiply any number with zero the resultant product will be zero.

Example: 2 x 0 = 0, 5 x 0 = 0, 9 x 0 = 0

If both numbers are zero, then the result also be zero.

0 x 0 = 0

Question 3:

If the product of two whole number is 1, can we say that one or both of them will be 1? Justify through examples.

SOLUTION 3:

If only one number be 1 then the product cannot be 1.

Examples: 5 x 1 = 5, 4 x 1 = 4, 8 x 1 = 8

If both number are 1, then the product is 1

1 x 1 = 1

Question 4:

Find using distributive property:

(a) 728 x 101

(b) 5437 x 1001

(d) 4275 x 125

(e) 504 x 35

SOLUTION 4:

(a) 728 x 101

= 728 x (100 + 1)

= 728 x 100 + 728 x 1

= 72800 + 728

= 73528

(b) 5437 x 1001

= 5437 x (1000 + 1)

= 5437 x 1000 + 5437 x 1

= 5437000 + 5437

= 5442437

= 824 x (20 + 5)

= 824 x 20 + 824 x 5

= 16480 + 4120

= 20600

(d) 4275 x 125

= 4275 x (100 + 20 + 5)

= 4275 x 100 + 4275 x 20 + 4275 x5

= 427500 + 85500 + 21375

= 534375

(e) 504 x 35

= (500 + 4) x 35

= 500 x 35 + 4 x 35

= 17500 + 140

= 17640

Question 5:

Study the pattern:

1 x 8 + 1 = 9;

12 x 8 + 2 = 98;

123 x 8 + 3 = 987

1234 x 8 + 4 = 9876;

12345 x 8 + 5 = 98765

Write the next two steps. Can you say how the pattern works?

SOLUTION 5:

123456 x 8 + 6 = 987654

1234567 x 8 + 7 = 9876543 Pattern works like this:

1 x 8 + 1 = 9

12 x 8 + 2 = 98

123 x 8 + 3 = 987

1234 x 8 + 4 = 9876

12345 x 8 + 5 = 98765

123456 x 8 + 6 = 987654

1234567 x 8 + 7 = 9875643

Class – 6 CH-1 KNOWING OUR NUMBERS NCERT SOLUTIONS

Class – 6 CH-1 KNOWING OUR NUMBERS

MATHS NCERT SOLUTIONS

EXERCISE 1.1

Question 1:

Fill in the blanks:

(a) 1 lakh = _______________ ten thousand

(b) 1 million = _______________ hundred thousand

(d) 1 crore = _______________ million

(e) 1 million = _______________ lakh

SOLUTION 1:

(a) 10

(b) 10

(d) 10

(e) 10

Question 2:

Place commas correctly and write the numerals:

(a) Seventy-three lakh seventy-five thousand three hundred seven.

(b) Nine crore five lakh forty-one.

(d) Fifty-eight million four hundred twenty-three thousand two hundred two.

(e) Twenty-three lakh thirty thousand ten.

SOLUTION 2:

(a) 73,75,307

(b) 9,05,00,041

(d) 58,423,202

(e) 23,30,010

Question 3:

Insert commas suitable and write the names according to Indian system of numeration:

(a) 87595762

(b) 8546283

(d) 98432701

SOLUTION 3:

(a) 8,75,95,762

Eight crore seventy-five lakh ninety-five thousand seven hundred sixty-two.

(b) 85,46,283

Eight-five lakh forty-six thousand two hundred eighty-three.

Nine crore ninety-nine lakh forty-six.

(d) 9,84,32,701

Nine crore eighty-four lakh thirty-two thousand seven hundred one.

Question 4:

Insert commas suitable and write the names according to International system of numeration:

(a) 78921092

(b) 7452283

(d) 48049831

SOLUTION 4:

(a) 78,921,092

Seventy-eight million nine hundred twenty-one thousand ninety-two

(b) 7,452,483

Seven million four hundred fifty-two thousand two hundred eighty-three

Ninety-nine million nine hundred eighty-five thousand one hundred two

(d) 48,049,831

Forty-eight million forty-nine thousand eight hundred thirty-one

Exercise 1.2

Question 1:

A book exhibition was held for four days in a school. The number of tickets sold at the counter on the first, second, third and final day was respectively 1094, 1812, 2050 and 2751. Find the total number of tickets sold on all the four days.

SOLUTION 1:

Number of tickets sold on first day = 1,094

Number of tickets sold on second day = 1,812

Number of tickets sold on third day = 2,050

Number of tickets sold on fourth day = + 2,751

Total tickets sold = 7,707

Therefore, 7,707 tickets were sold on all the four days.

Question 2:

Shekhar is a famous cricket player. He has so far scored 6980 runs in test matches. He wishes to complete 10,000 runs. How many more runs does he need?

SOLUTION 2:

Runs to achieve = 10,000

Runs scored = – 6,980

Runs required = 3,020

Therefore, he needs 3,020 more runs.

Question 3:

In an election, the successful candidate registered 5,77,500 votes and his nearest rival secured 3,48,700 votes. By what margin did the successful candidate win the election?

SOLUTION 3:

Number of votes secured by successful candidates = 5,77,500

Number of votes secured by his nearest rival = – 3,48,700

Margin between them = 2,28,800

Therefore, the successful candidate won by a margin of 2,28,800 votes.

Question 4:

Kirti Bookstore sold books worth ₹2,85,891 in the first week of June and books worth ₹4,00,768 in the second week of the month. How much was the sale for the two weeks together? In which week was the sale greater and by how much?

SOLUTION 4:

Books sold in first week = 2,85,891

Books sold in second week = + 4,00,768

Total books sold = 6,86,659

Since, 4,00,768,> 2,85,891

Therefore sale of second week is greater than that of first week.

Books sold in second week = 4,00,768

Books sold in first week = – 2,85,891

More books sold in second week = 1,14,877

Therefore, 1,14,877 more books were sold in second week.

Question 5:

Find the difference between the greatest and the least number that can be written using the digits 6, 2, 7, 4, 3 each only once.

SOLUTION 5:

Greatest five-digit number using digits 6,2,7,4,3 = 76432

Smallest five-digit number using digits 6,2,7,4,3 = – 23467

Difference = 52965

Therefore the difference is 52965.

Question 6:

A machine, on an average, manufactures 2,825 screws a day. How many screws did it produce in the month of January 2006?

SOLUTION 6:

Number of screws manufactured in one day = 2,825

Number of days in the month of January (31 days) = 2,825 x 31 = 87,575

Therefore, the machine produced 87,575 screws in the month of January.

Question 7:

A merchant had ₹78,592 with her. She placed an order for purchasing 40 radio sets at ₹1,200 each. How much money will remain with her after the purchase?

SOLUTION 7:

Cost of one radio = ₹ 1200

Cost of 40 radios = 1200 x 40

Now, = ₹ 48,000

Total money with merchant = ₹ 78,592

Money spent by her = – ₹ 48,000

Money left with her = ₹ 30,592

Therefore, ₹ 30,592 will remain with her after the purchase.

Question 8:

A student multiplied 7236 by 65 instead of multiplying by 56. By how much was his answer greater than the correct answer?

SOLUTION 8:

Wrong answer = 7236 x 65 = 470340

Correct answer = 7236 x 56 =405216

Difference in answers = 470340 – 405216 = 65,124

Question 9:

To stitch a shirt 2 m 15 cm cloth is needed. Out of 40 m cloth, how many shirts can be stitched and how much cloth will remain?

SOLUTION 9:

Cloth required to stitch one shirt = 2 m 15 cm

= 2 x 100 cm + 15 cm

= 215 cm

Length of cloth = 40 m = 40 x 100 cm = 4000 cm

Number of shirts can be stitched = 4000 ÷ 215

Therefore, 18 shirts can be stitched and 130 cm (1 m 30 cm) cloth will remain.

Question 10:

Medicine is packed in boxes, each weighing 4 kg 500 g. How many such boxes can be loaded in a can which cannot carry beyond 800 kg?

SOLUTION 10:

The weight of one box = 4 kg 500 g = 4 x 1000 g + 500 g = 4500 g

Maximum load can be loaded in van = 800 kg = 800 x 1000 g = 800000 g

Number of boxes = 800000 ÷ 4500

Therefore, 177 boxes can be loaded.

Question 11:

The distance between the school and the house of a student’s house is 1 km 875 m. Every day she walks both ways. Find the total distance covered by her in six days.

SOLUTION 11:

Distance between school and home = 1.875 km

Distance between home and school = + 1.875 km

Total distance covered in one day = 3.750 km

Distance covered in six days = 3.750 x 6 = 22.500 km

Therefore, 22 km 500 m distance covered in six days.

Question 12:

A vessel has 4 litres and 500 ml of curd. In how many glasses each of 25 ml capacity, can it be filled?

SOLUTION 12:

Capacity of curd in a vessel = 4 litres 500 ml = 4 x 1000 ml + 500 ml = 4500 ml

Capacity of one glass = 25 ml

Number of glasses can be filled = 4500 ÷ 25

Therefore, 180 glasses can be filled by curd.

Exercise 1.3

Question 1:

Estimate each of the following using general rule:

(a) 730 + 998

(b) 796 – 314

(d) 28,292 – 21,496

SOLUTION 1:

(a) 730 round off to 700

998 round off to 1000

Estimated sum = 1700

(b) 796 round off to 800

314 round off to 300

Estimated sum = 500

2888 round off to 3000

Estimated sum = 16000

(d) 28292 round off to 28000

21496 round off to 21000

Estimated difference = 7000

Question 2:

Give a rough estimate (by rounding off to nearest hundreds) and also a closer estimate (by rounding off to nearest tens):

(a) 439 + 334 + 4317

(b) 1,08,737 – 47,599

(d) 4,89,348 – 48,365

SOLUTION 2:

(a) 439 round off to 400

334 round off to 300

4317 round off to 4300

Estimated sum = 5000

(b) 108734 round off to 108700

47599 round off to 47600

Estimated difference = 61100

491 round off to 500

Estimated difference = 7800

(d) 489348 round off to 489300

48365 round off to 48400

Estimated difference = 440900

Question 3:

Estimate the following products using general rule:

(a) 578 x 161

(b) 5281 x 3491

(d) 9250 x 29

SOLUTION 3:

(a) 578 x 161

578 round off to 600

161 round off to 200

The estimated product = 600 x 200 = 1,20,000

(b) 5281 x 3491

5281 round of to 5,000

3491 round off to 3,500

The estimated product = 5,000 x 3,500 = 1,75,00,000

1291 round off to 1300

592 round off to 600

The estimated product = 1300 x 600 = 7,80,000

(d) 9250 x 29

9250 round off to 10,000

229 round off to 30

The estimated product = 10,000 x 30 = 3,00,000