CLASS 11 NCERT SETS NOTES 

SETS

THE EMPTY SET, SINGLETON SET, FINITE AND INFINITE SETS, CARDINAL NUMBER OF A FINITE SET, EQUIVALENT SETS, EQUAL SETS

SUBSET, PROPER SUBSET, SUPER SET, UNIVERSAL SET, INTERVAL AS A SUBSET OF REAL NUMBERS

INTERVAL AS A SUBSET OF REAL NUMBERS

CLASS 11 SETS NOTES

 A set is a well-defined collection of objects. 

There are two methods of representing a set : 

(i) Roster or tabular form 

(ii) Set-builder form. 

(i) In roster form, all the elements of a set are listed, the elements are being separated by commas and are enclosed within braces { }.

In roster form, the order in which the elements are listed is immaterial. 

It may be noted that while writing the set in roster form an element is not generally repeated, i.e., all the elements are taken as distinct

In set-builder form,

all the elements of a set possess a single common property which is not possessed by any element outside the set.

If a is an element of a set A, we say that “ a belongs to A” the Greek symbol ∈ (epsilon) is used to denote the phrase ‘belongs to’. Thus, we write a ∈ A. If ‘b’ is not an element of a set A, we write b ∉ A and read “b does not belong to A”

E.g {x:x is a vowel in English alphabet} 

In this description the braces stand for “the set of all”, the colon stands for “such that”

empty set or the null set or the void set

A set which does not contain any element is called the empty set or the null set or the void set. The empty set is denoted by the symbol φ or { }

 number of distinct elements of the set and we denote it by n (S). If n (S) is a natural number, then S is non-empty finite set

A set which is empty or consists of a definite number of elements is called finite otherwise, the set is called infinite. 

All infinite sets cannot be described in the roster form. For example, the set of real numbers cannot be described in this form, because the elements of this set do not follow any particular pattern.

Equal Sets - Two sets A and B are said to be equal if they have exactly the same elements and we write A = B. Otherwise, the sets are said to be unequal and we write A ≠ B.

A set does not change if one or more elements of the set are repeated.

 The symbol ⊂ stands for ‘is a subset of’ or ‘is contained in’.

A set A is said to be a subset of a set B if every element of A is also an element of B.

 In other words, A ⊂ B if whenever a ∈ A, then a ∈ B. 

It is often convenient to use the symbol “⇒” which means implies.

A ⊂ B if a ∈ A ⇒ a ∈ B 

“A is a subset of B if a is an element of A implies that a is also an element of B”. 

If A is not a subset of B, we write A ⊄ B.

In this case, A and B are the same sets so that we have A ⊂ B and B ⊂ A ⇔ A = B, where “⇔” is a symbol for two way implications, and is usually read as if and only if (briefly written as “iff”). 

Every set A is a subset of itself, i.e., A ⊂ A. 

Since the empty set φ has no elements, φ is a subset of every set

proper subset

Let A and B be two sets. If A ⊂ B and A ≠ B , then A is called a proper subset of B and B is called superset of A. 

For example, A = {1, 2, 3} is a proper subset of B = {1, 2, 3, 4}. 

If a set A has only one element, we call it a singleton set. Thus,{ a } is a singleton set.

Example 11 Let A, B and C be three sets. If A ∈ B and B ⊂ C, is it true that A ⊂ C?. If not, give an example.

Solution 

No. 

Let A = {1}, B = {{1}, 2} and C = {{1}, 2, 3}. 

Here A ∈ B as A = {1} and B ⊂ C. 

But A ⊄ C as 1 ∈ A and 1 ∉ C. 

Note that an element of a set can never be a subset of itself.

The number (b – a) is called the length of any of the intervals (a, b), [a, b], [a, b) or (a, b].

R Let a, b ∈ R and a < b.

 Then the set of real numbers { y : a < y < b} is called an open interval and is denoted by (a, b).

 All the points between a and b belong to the open interval (a, b) but a, b themselves do not belong to this interval.

 The interval which contains the end points also is called closed interval and is denoted by [ a, b ]. 

Thus [ a, b ] = {x : a ≤ x ≤ b} 

Intervals closed at one end and open at the other, i.e., [ a, b ) = {x : a ≤ x < b} is an open interval from a to b, including a but excluding b. 

( a, b ] = { x : a < x ≤ b } is an open interval from a to b including b but excluding a.

 These notations provide an alternative way of designating the subsets of set of real numbers.

 For example , if A = (–3, 5) and B = [–7, 9], then A ⊂ B. 

The set [ 0, ∞) defines the set of non-negative real numbers, 

while set ( – ∞, 0 ) defines the set of negative real numbers. 

The set ( – ∞, ∞ ) describes the set of real numbers in relation to a line extending from – ∞ to ∞

U

This basic set is called the “Universal Set”. The universal set is usually denoted by U

VENN DIAGRAMS & UNION SETS

Most of the relationships between sets can be represented by means of diagrams which are known as Venn diagrams.

The universal set is represented usually by a rectangle and its subsets by circles.

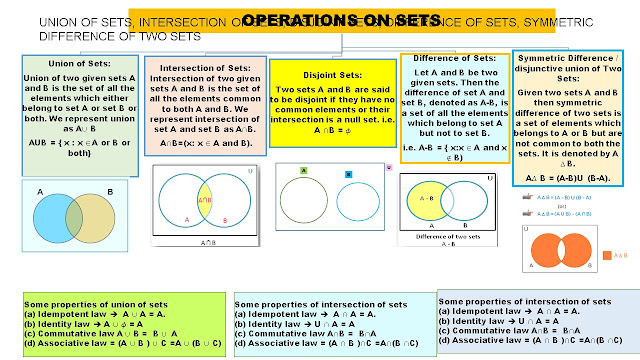
Let A and B be any two sets. The union of A and B is the set which consists of all the elements of A and all the elements of B, the common elements being taken only once. The symbol ‘∪’ is used to denote the union. Symbolically, we write A ∪ B and usually read as ‘A union B’

The union of two sets A and B is the set C which consists of all those elements which are either in A or in B (including those which are in both). In symbols, we write. A ∪ B = { x : x ∈A or x ∈B }

Some Properties of the Operation of Union

 (i) A ∪ B = B ∪ A (Commutative law) 

(ii) ( A ∪ B ) ∪ C = A ∪ ( B ∪ C) (Associative law ) 

(iii) A ∪ φ = A (Law of identity element, φ is the identity of ∪)

(iv) A ∪ A = A (Idempotent law)

 (v) U ∪ A = U (Law of U)

INTERSECTION

The intersection of sets A and B is the set of all elements which are common to both A and B. The symbol ‘∩’ is used to denote the intersection. The intersection of two sets A and B is the set of all those elements which belong to both A and B. Symbolically, we write A ∩ B = {x : x ∈ A and x ∈ B}.

Some Properties of Operation of Intersection

 (i) A ∩ B = B ∩ A (Commutative law). 

(ii) ( A ∩ B ) ∩ C = A ∩ ( B ∩ C ) (Associative law). 

(iii) φ ∩ A = φ, U ∩ A = A (Law of φ and U). 

(iv) A ∩ A = A (Idempotent law)

(v) A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C ) (Distributive law ) i. e., ∩ distributes over ∪

DISJOINT SETS

 If A and B are two sets such that A ∩ B = φ, then A and B are called disjoint sets

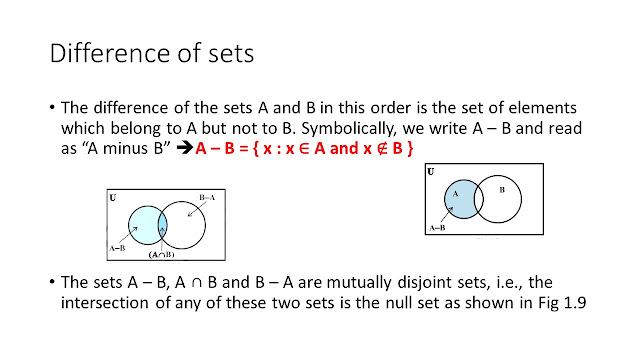
Difference of sets

The difference of the sets A and B in this order is the set of elements which belong to A but not to B. Symbolically, we write A – B and read as “A minus B” A – B = { x : x ∈ A and x ∉ B }

The sets A – B, A ∩ B and B – A are mutually disjoint sets, i.e., the intersection of any of these two sets is the null set as shown in Fig 1.9

Complement of a Set

Let U be the universal set and A a subset of U. Then the complement of A is the set of all elements of U which are not the elements of A. 

Symbolically, we write A′ to denote the complement of A with respect to U. 

Thus, A′ = {x : x ∈ U and x ∉ A }. Obviously A′ = U – A We note that the complement of a set A can be looked upon, alternatively, as the difference between a universal set U and the set A.

If A and B are any two subsets of the universal set U, then ( A ∪ B )′ = A′ ∩ B′. Similarly, ( A ∩ B )′ = A′ ∪ B′

If A is a subset of the universal set U, then its complement A′ is also a subset of U. 

( A′)′ = A

The complement of the union of two sets is the intersection of their complements and the complement of the intersection of two sets is the union of their complements. These are called De Morgan’s laws. These are named after the mathematician De Morgan

Some Properties of Complement Sets

 1. Complement laws: 

(i) A ∪ A′ = U (ii) A ∩ A′ = φ 

2. De Morgan’s law: 

(i) (A ∪ B)´ = A′ ∩ B′ 

(ii) (A ∩ B)′ = A′ ∪ B′ 

3. Law of double complementation : (A′)′ = A 

4. Laws of empty set and universal set φ′ = U and U′ = φ