Class – 6 CH-6 INTEGERS

MATHS NCERT SOLUTIONS

Exercise 6.1

Question 1 :

Write opposite of the following:

(a) Increase in weight

(b) 30 km north

(d) Loss of ₹700

(e) 100 m above sea level

Solution 1:

(a) Decrease in weight

(b) 30 km south

(d) Profit of ₹700

(e) 100 m below sea level

Question 2:

Represent the following numbers as integers with appropriate signs.

(a) An aeroplane is flying at a height two thousand meters above the ground.

(b) A submarine is moving at a depth eight thousand meters below the sea level.

(d) Withdrawal of rupees seven hundred.

Solution 2:

(a) (+) 200 meters

(b) (–) 800 meters

(d) (–) 700 Rupees

Question 3:

Represent the following numbers on number line:

(a) +5

(b) –10

(d) –1

(e) –6

Solution 3:

(a)

Question 4:

Adjacent figure is a vertical number line, representing integers. Observe it and locate the following

points:

(a) If point D is +8 then which point is –8?

(b) Is point G a negative integer or a positive integer?

(d) Which point marked on this number line has the least value?

(e) Arrange all the points in decreasing order of values.

Solution 4:

(a) F

(b) Negative

(d) E

(e) D, C, B, A, O, H, G, F, E

Question 5:

Following is the list of temperatures of five places in India, on a particular day of the year.

Place Temperature

Siachin 10°C below 0°C ____________________

Shimla 2°C below 0°C ____________________

Ahmedabad 30°C above 0°C ____________________

Delhi 20°C above 0°C ____________________

Srinagar 5°C below 0°C ____________________

(a) Write the temperature of these places in the form of integers in the blank column.

(b) Following is the number line representing the temperature in degree Celsius.

Plot the name of the city against its temperature.

(d) Write the names of the place where temperature are above 10°C.

Solution 5:

Place Temperature

(a) Siachin (–) 10°C

Shimla (–) 2°C

Ahmedabad (+) 30°C

Delhi (+) 20°C

Srinagar (–) 5°C

(b) Number line

(d) Ahemadabad and Delhi

Question 6:

In each of the following pairs, which number is to the right of the other on the number line?

(a) 2, 9

(b) –3, –8

(d) –11, 10

(e) –6, 6

(f) 1, –100

Solution 6:

(a) 9 is right to 2

(b) –3 is right to –8

(d) 10 is right to –11

(e) 6 is right to –6

(f) 1 is right to –100

Question 7:

Write all the integers between the given pairs (write them in the increasing order):

(a) 0 and –7

(b) –4 and 4

(d) –30 and –23

Solution 7:

(a) –6, –5, –4, –3, –2, –1

(b) –3, –2, –1, 0, 1, 2, 3

(d) –29, –28, –27, –26, –25, –24

Question 8:

(a) Write four negative integers greater than –20.

(b) Write four negative integers less than –10.

Solution 8:

(a) –19, –18, –17, –16

(b) –11, –12, –13, –14

Question 9:

For the following statements write True (T) or False (F). If the statement is false, correct the statement:

(a) –8 is to the right of –10 on a number line.

(b) –100 is the right of –50 on a number line.

(d) –26 is larger than –25.

Solution 9:

(a) True

(b) False

(d) False

Question 10:

Draw a number line and Solution the following:

(a) Draw a number line will we reach if we move 4 numbers to the right of –2.

(b) Which number will we reach if we move 5 numbers to the left of 1.

(d) If we are at –6 on the number line, in which direction should we move to reach –1?

Solution 10:

(d) On right side

Exercise 6.2

Question 1:

Using the number line write the integer which is:

(a) 3 more than 5

(b) 5 more than –5

(d) 3 less than –2

Solution 1:

(a) 8

(b) 0

(d) –5

Question 2:

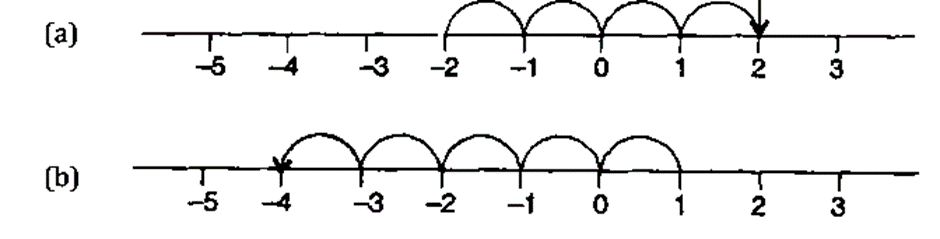
Use number line and add the following integers:

(a) 9 + (–6)

(b) 5 + (–11)

(d) (–5) + 10

(e) (–1) + (–2) + (–3)

(f) (–2) + 8 + (–4)

Solution 2:

(a) 9 + (–6) = 3

(b) 5 + (–11) = –6

(d) (–5) + 10 = 5

(e) (–1) + (–2) + (–3) = –6

(f) (–2) + 8 + (–4) = 2

Question 3:

Add without using number line:

(a) 11 + (–7)

(b) (–13) + (+18)

(d) (–250) + (+150)

(e) (–380) + (–270)

(f) (–217) + (–100)

Solution 3:

(a) 11 + (–7) = 11 – 7 = 4

(b) (–13) + 18 = 5

(d) (–250) + (+150) = –250 + 150 = –100

(e) (–380) + (–270) = –380 – 270 = –650

(f) (–217) + (–100) = –217 - 100 = –317

Question 4:

Find the sum of:

(a) 137 and –354

(b) –52 and 52

(d) –50, –200 and 300

Solution 4:

(a) 137 + (–354) = 137 – 354 = –217

(b) (–52) + 52 = 0

(d) (–50) + (–200) + 300 = –50 – 200 + 300 = –250 + 300 = 50

Question 5:

Find the value of:

(a) (–7) + (–9) + 4 + 16 (b) 37 + (–2) + (–65) + (–8)

Solution 5:

(a) (–7) + (–9) + 4 + 16

= –7 – 9 + 4 + 16

= –16 + 20

= 4

(b) 37 + (–2) + (–65) + (–8)

= 37 – 2 – 65 – 8

= 37 – 75

= –38

Exercise 6.3

Question 1:

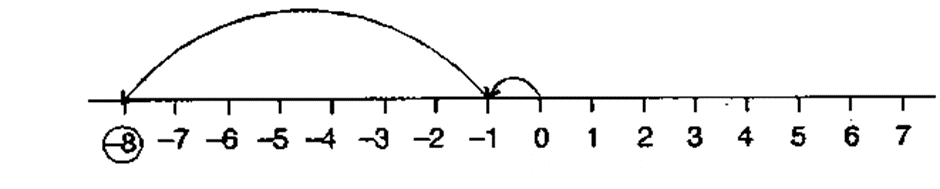
Subtract:

(a) 35 – (20)

(b) 72 – (90)

(d) (–20) – (13)

(e) 23 – (–12)

(f) (–32) – (–40)

Solution 1:

(a) 35 – 20 = 15

(b) 72 – 90 = –18

(d) –20 – (13) = –20 – 13 = –33

(e) 23 – (–12) = 23 + 12 = 35

(f) (–32) – (–40) = –32 + 40 = 8

Question 2:

Fill in the blanks with >, < or = sign:

(a) (–3) + (–6) _______________ (–3) – (–6)

(b) (–21) – (–10) _______________ (–31) + (–11)

Solution 2:

(a) (–3) + (–6) <(–3) – (–6)

(b) (–21) – (–10) > (–31) + (–11)

(d) (–25) – (–42) > (–42) – (–25)

Question 3:

Fill in the blanks:

(a) (–8) + __________ = 0

(b) 13 + __________ = 0

(d) (–4) + __________ = –12

(e) __________ – 15 = –10

Solution 3:

(a) (–8) + 8 = 0

(b) 13 + (–13) = 0

(d) (–4) + (–8) = –12

(e) 5 – 15 = –10

Question 4:

Find:

(a) (–7) – 8 – (–25)

(b) (–13) + 32 – 8 – 1

(d) 50 – (–40) – (–2)

Solution 4:

(a) (–7) – 8 – (–25)

= –7 – 8 + 25

= –15 + 25

= 10

(b) (–13) + 32 – 8 – 1

= –13 + 32 – 8 – 1

= 32 – 22

= 10

= –7 – 8 – 90

= –105

(d) 50 – (–40) – (–2)

= 50 + 40 + 2

= 92

Sunday, December 17, 2023