Class 09 To verify the algebraic identity :a3 – b3 = (a – b)(a2 + ab + b2)

 

Activity 10

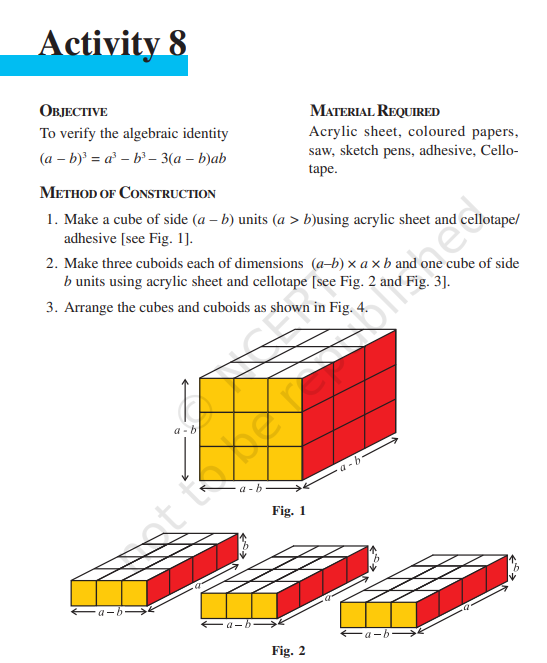
OBJECTIVE

To verify the algebraic identity :a³ – b³ = (a – b)(a² + ab + b²)

 METHOD OF CONSTRUCTION

MATERIAL REQUIRED

Acrylic sheet, sketch pen, glazed papers, scissors, adhesive, cello-tape, coloured papers, cutter.

1.   Make a cuboid of dimensions (a–b) × a × a (b < a), using acrylic sheet and cellotape/adhesive as shown in Fig. 1.

 2.   Make another cuboid of dimensions (a–b) × a × b, using acrylic sheet and cellotape/adhesive as shown in Fig. 2.

 3.   Make one more cuboid of dimensions (a–b) × b × b as shown in Fig. 3.

 4.    Make a cube of dimensions b × b × b using acrylic sheet as shown in Fig. 4.

5.   Arrange the cubes and cuboids made above in Steps (1), (2), (3) and (4) to obtain a solid as shown in Fig. 5, which is a cube of volume a³ cubic units.

Fig. 5

 Fig. 6

 DEMONSTRATION

 Volume of cuboid in Fig. 1 = (a–b) × a × a cubic units.

 Volume of cuboid in Fig. 2 = (a–b) × a × b cubic units.

 Volume of cuboid in Fig. 3 = (a–b) × b × b cubic units.

 Volume of cube in Fig. 4 = b³ cubic units.

 Volume of solid in Fig. 5 = a³ cubic units.

 Removing a cube of size b³ cubic units from the solid in Fig. 5, we obtain a solid as shown in Fig. 6.

 Volume of solid in Fig. 6 = (a–b) a² + (a–b) ab + (a–b) b²

 =  (a–b) (a² + ab + b²)

 Therefore, a³ – b³ = (a – b)(a² + ab + b²)

OBSERVATION

 On actual measurement:

 a = ..............,        b = ..............,

 So, a³ = ..............,       b³ = .............., (a–b) = ..............,    ab = ..............,

 a²  = ..............,      b² = ..............,

 Therefore, a³ – b³ = (a – b) (a² + ab + b²).

 APPLICATION

 The identity may be used in simplification/factorisation of algebraic expressions.

Class 09 To verify the algebraic identity (a – b)3 = a3 – b3 – 3(a – b)ab

 Activity 8 

OBJECTIVE	MATERIAL REQUIRED
To verify the algebraic identity	Acrylic sheet, coloured papers,
(a – b)3 = a3 – b3 – 3(a – b)ab	saw, sketch pens, adhesive, Cello-
	tape.
METHOD OF CONSTRUCTION

 1.   Make a cube of side (a – b) units (a > b)using acrylic sheet and cellotape/ adhesive [see Fig. 1].

2.   Make three cuboids each of dimensions (a–b) × a × b and one cube of side b units using acrylic sheet and cellotape [see Fig. 2 and Fig. 3].

 Arrange the cubes and cuboids as shown in Fig. 4.

DEMONSTRATION

Volume of the cube of side (a – b) units in Fig. 1 = (a– b)³ Volume of a cuboid in Fig. 2 = (a–b) ab

Volume of three cuboids in Fig. 2 = 3 (a–b) ab Volume of the cube of side b in Fig. 3 = b³

Volume of the solid in Fig. 4 = (a–b)³ + (a–b) ab + (a–b) ab + (a – b) ab + b³

= (a–b)3 + 3(a–b) ab + b3	(1)
Also, the solid obtained in Fig. 4 is a cube of side a
Therefore, its volume = a3	(2)
From (1) and (2),
(a–b)3 + 3(a–b) ab + b3 = a3
or (a–b)3 = a3 – b3 – 3ab (a–b).
Here, volume is in cubic units.

OBSERVATION

 On actual measurement:

 a = ..............,            b = ..............,       a–b = ..............,

 So, a³ = ..............,       ab = ..............,

b³ = ..............,       ab(a–b) = ..............,

 3ab (a–b) = ..............,     (a–b)³ = ..............,

 Therefore, (a–b)³ = a³ – b³ – 3ab(a–b)

 APPLICATION

 The identity may be used for

 1.   calculating cube of a number expressed as a difference of two convenient numbers

 simplification and factorisation of algebraic expressions.

NOTE

 This identity can also be expressed as : (a – b)³ = a³ – 3a²b + 3ab² – b³.

Class 09 To verify the algebraic identity :(a+b)3 = a3 + b3 + 3a2b + 3ab2

 Activity 7

OBJECTIVE                

                                            

To verify the algebraic identity :(a+b)³ = a³ + b³ + 3a²b + 3ab²

 MATERIAL REQUIRED

Acrylic sheet, coloured papers, glazed papers, saw, sketch pen, adhesive, Cello-tape.

METHOD OF CONSTRUCTION

1.   Make a cube of side a units and one more cube of side b units (b < a), using acrylic sheet and cello-tape/adhesive [see Fig. 1 and Fig. 2].

 Similarly, make three cuboids of dimensions a×a×b and three cuboids of dimensions a×b×b [see Fig. 3 and Fig. 4].

3. Arrange the cubes and cuboids as shown in Fig. 5.

DEMONSTRATION

 Volume of the cube of side a = a×a×a = a³, volume of the cube of side b = b³ Volume of the cuboid of dimensions a×a×b = a²b, volume of three such cuboids

=   3a²b

 Volume of the cuboid of dimensions a×b×b = ab², volume of three such cuboids

=   3ab²

 Solid figure obtained in Fig. 5 is a cube of side (a + b)

 Its volume = (a + b)³

 Therefore, (a+b)³ = a³ + b³ + 3a²b + 3ab²

 Here, volume is in cubic units.

 OBSERVATION

 On actual measurement:

 a = ..............,         b = ............., a³  = ..............,

 So, a³ = ..............,       b³  = ............., a²b = ..............,            3a²b= ..............,

 ab² = ..............,   3ab² = ..............,          (a+b)³ = ..............,

 Therefore, (a+b)³ = a³ + b³ +3a²b + 3ab²

 APPLICATION

 The identity may be used for

 1.   calculating cube of a number expressed as the sum of two convenient numbers

 simplification and factorisation of algebraic expressions