Class 09 To verify the algebraic identity (a – b)3 = a3 – b3 – 3(a – b)ab

 Activity 8 

OBJECTIVE	MATERIAL REQUIRED
To verify the algebraic identity	Acrylic sheet, coloured papers,
(a – b)3 = a3 – b3 – 3(a – b)ab	saw, sketch pens, adhesive, Cello-
	tape.
METHOD OF CONSTRUCTION

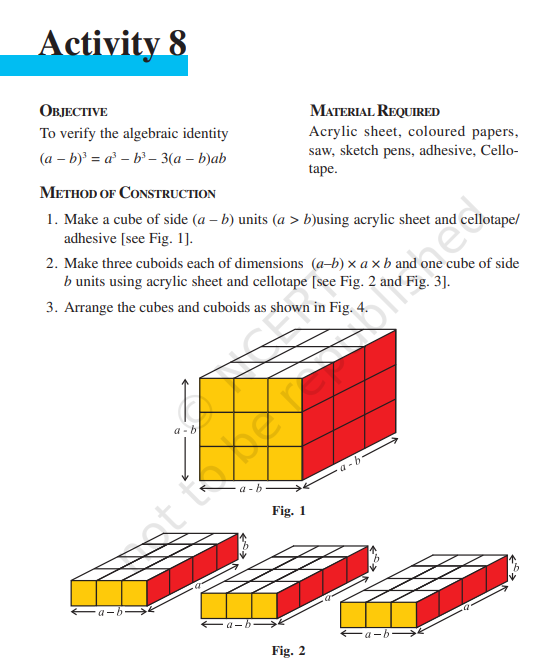
 1.   Make a cube of side (a – b) units (a > b)using acrylic sheet and cellotape/ adhesive [see Fig. 1].

2.   Make three cuboids each of dimensions (a–b) × a × b and one cube of side b units using acrylic sheet and cellotape [see Fig. 2 and Fig. 3].

 Arrange the cubes and cuboids as shown in Fig. 4.

DEMONSTRATION

Volume of the cube of side (a – b) units in Fig. 1 = (a– b)³ Volume of a cuboid in Fig. 2 = (a–b) ab

Volume of three cuboids in Fig. 2 = 3 (a–b) ab Volume of the cube of side b in Fig. 3 = b³

Volume of the solid in Fig. 4 = (a–b)³ + (a–b) ab + (a–b) ab + (a – b) ab + b³

= (a–b)3 + 3(a–b) ab + b3	(1)
Also, the solid obtained in Fig. 4 is a cube of side a
Therefore, its volume = a3	(2)
From (1) and (2),
(a–b)3 + 3(a–b) ab + b3 = a3
or (a–b)3 = a3 – b3 – 3ab (a–b).
Here, volume is in cubic units.

OBSERVATION

 On actual measurement:

 a = ..............,            b = ..............,       a–b = ..............,

 So, a³ = ..............,       ab = ..............,

b³ = ..............,       ab(a–b) = ..............,

 3ab (a–b) = ..............,     (a–b)³ = ..............,

 Therefore, (a–b)³ = a³ – b³ – 3ab(a–b)

 APPLICATION

 The identity may be used for

 1.   calculating cube of a number expressed as a difference of two convenient numbers

 simplification and factorisation of algebraic expressions.

NOTE

 This identity can also be expressed as : (a – b)³ = a³ – 3a²b + 3ab² – b³.