Class 06 To determine the number of lines of symmetry of the following shapes by paper folding

 MATHS ACTIVITIES

CLASS 6

Based on CHAPTERs

9.data handling

10. mensuration

13. symmetry

14. practical geometry

ACTIVITY - SYMMETRY

Objective: 

To determine the number of lines of symmetry of the following shapes by paper folding

(a) equilateral triangle (b) isosceles triangle (c) square(d) rectangle (e) rhombus

Materials Required: 

White sheets of paper, tracing paper, a pair of scissors, geometry box, etc.

Procedure:

1.Trace each of the following shapes on a separate tracing paper.

(A) Equilateral Triangle (B) Isosceles Triangle (C) Square  (D) Rectangle (E) Rhombus

ACTIVITY - SYMMETRY

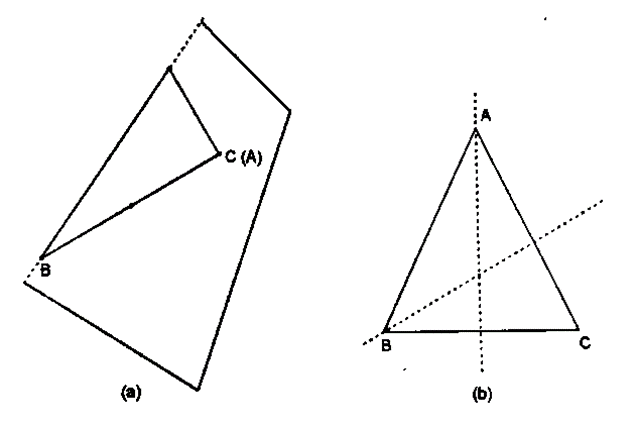
2. Fold the equilateral triangle ABC at A such that vertex B coincides with vertex C. We see that the two parts of the triangle exactly cover each other.

3. Unfold it and draw a dotted line along the crease.

4. Now, fold the triangle ABC at B such that A and C coincide. Here also, the two parts of the triangle cover each other exactly. Unfold it and draw a dotted line along the crease.

ACTIVITY - SYMMETRY

5. Similarly, fold the triangle at C such that vertex A coincides with vertex B. The two parts of triangle ABC cover each other exactly. Unfold it and draw a dotted line along the crease.

6. Take the isosceles triangle DEF and fold it at D such that vertex E coincides with vertex F.

We see that the two parts of ADEF cover each other exactly.

 Unfold it and draw a dotted line along the crease.

ACTIVITY - SYMMETRY

7. Now, fold the ADEF first at E and then at F. You will see that in each case the two parts of ADEF do not cover each other exactly.

8. Take the square PQRS and fold it from the middle such that S coincides with R and P coincides with Q. In this case the two parts of the square PQRS cover each other exactly. Unfold it and draw a dotted line along the crease. 

9. Again fold the square PQRS from the middle such that S coincides with P and R coincides with Q. Here also the two parts cover each other exactly. Unfold it and draw a dotted line along the crease.

ACTIVITY - SYMMETRY

10. Fold the square PQRS such that the folding  line passes through P and R. We see that the two parts of the square cover each other exactly. Unfold it and draw a dotted line along the crease.

11. Now fold the square PQRS such that the folding  line passes through Q and S. We see that the two parts of the square cover each other exactly. /Unfold it and draw a dotted line along the crease.

12. Take the rectangle IJKL and fold it from the middle such that L coincides with K and I coincides with J. Here the two parts of the rectangle cover each other exactly. Unfold it and draw a dotted line along the crease.

ACTIVITY - SYMMETRY

13. Fold the rectangle IJKL from the middle such that K  coincides with J and L coincides with I. here also the two parts cover each exactly. Unfold it and draw a dotted line along the crease.

14. If we fold the rectangle such that the folding time passes through I and K, the two parts do not cover each other exactly. Similarly, on folding the rectangle along JL, the two parts do not cover each other exactly.

15. Take from rhombus WXYZ and fold it so that the folding line passes through Z and X. We see the two parts of the rhombus exactly cover each other. Unfold it and draw a dotted line along the crease.

16. Fold parts the rhombus WXYZ such that folding line passes through W and Y. Here also the two parts cover each other exactly. Unfold it and draw a dotted line along the crease.

ACTIVITY - SYMMETRY

Observations:

 1. We observe that each dotted line in figure, divides the triangle into two identical parts. Hence, each dotted line is a line of symmetry of the equilateral triangle ABC. 

2.In figure, the dotted line divides the isosceles triangle DEF in two identical parts. Hence, it is a line of symmetry of triangle DEF.

 3. In figure, each of the four dotted lines divides the square into two identical parts. So each dotted line is a line of symmetry of the square PQRS.

4. In figure, each of the four dotted lines divides the rectangle IJKL into two identical parts. So each dotted line is a line of symmetry of the rectangle IJKL.

5. In figure, each of the four dotted lines divides the rhombus WXYZ into two identical parts. So each dotted line is a line of symmetry of the rhombus WXYZ.

Hence each dotted line is a line of symmetry of the rhombus WXYZ.

Conclusion:

A square has 4  lines of has symmetry

An equilateral triangle 3 lines of symmetry.

An isosceles triangle has only one. line of symmetry.

4. A rectangle has 2 lines of symmetry. 

5. A rhombus has 2 lines of symmetry.

Do Yourself : 

Find the number  of lines of symmetry of each of the shapes  given above by taking different dimensions by paper of folding.