MATHS ACTIVITIES��
ACTIVITY – WHOLE NUMBERS
CLASS 6�
Based on CHAPTERs�
2.WHOLE NUMBERS�
6.INTEGERS�
7.FRACTIONS�
8.DECIMALS��
Objective.:
To verify that addition is commutative for whole numbers by paper cutting and pasting method
Materials Required: Squared paper, colour pencils, a pair of scissors, glue stick, geometry box, etc.
Procedure:
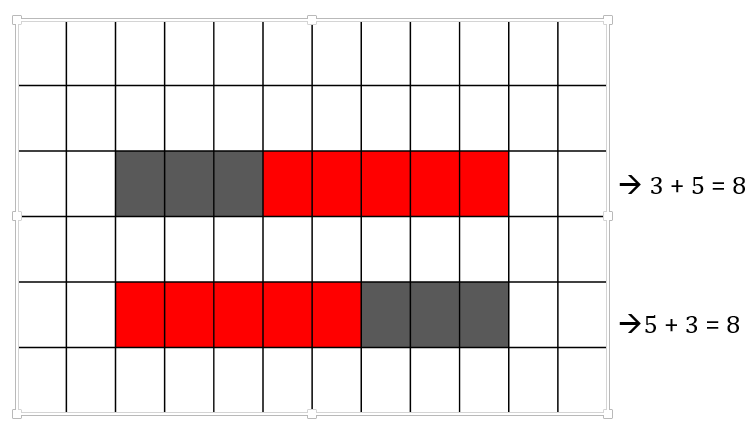
On a squared paper, colour 3 squares black as shown below.
3 + 5= 8
2. In the same row, colour 5 squares red.
In all there are 8 coloured squares.
3. Colour 5 squares red as shown below.
4. In the same row, colour 3 squares black. Here also, there are 8 coloured squares.ACTIVITY – WHOLE NUMBERS
5. Cut out both the coloured strips and paste them together on a sheet of paper as shown below
ACTIVITY – WHOLE NUMBERS
6. Repeat steps 1 to 5 to add 6 and 9.
ACTIVITY – WHOLE NUMBERS
Observations:
In step 5, the length of both the strips is same.
In the first strip, there are 8 coloured squares, out of which 3 are black and 5 are red.
So it shows 3 + 5 = 8
2. In the second strip, there are 8 coloured squares, out of which 5 are red and 3 are black.
So it shows 5 + 3 =8.
Thus, we have 3 + 5 = 8 = 5 + 3
3. Similarly, from figure 10, we can say that 6 + 9 = 9+ 6
Conclusion:
From the above activity, we can say that, the addition of whole numbers is commutative. i.e. two whole numbers can be added in any order sum remains the same.
Do Yourself :
Verify the commutative. property of addition of whole numbers by taking the following pairs of whole numbers
1. 4 and 7
2. 5 and 8
3. 6 and 7
4. 10 and 6
5. 15 and 3





No comments:
Post a Comment