ACTIVITY3 - LINES AND ANGLES
Objective:
To verify that if two parallel lines are cut by a transversal, then each pair of interior angles on the same side of the transversal are supplementary by paper cutting and pasting
Materials Required:
White sheets of paper, colour pencils, geometry box, a pair of scissors, gluestick, etc.
Procedure:
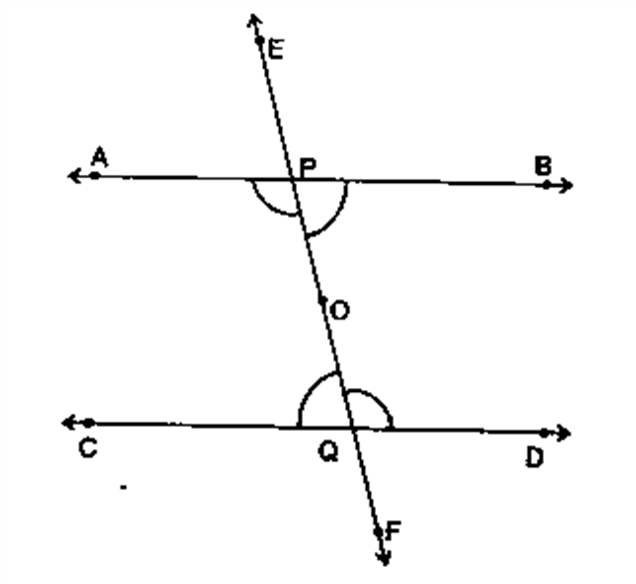
1. cutting On a white sheet of paper, draw two parallel lines AB and CD and a transversal EF cutting them at P and Q resp., Mark a point O on PQ.
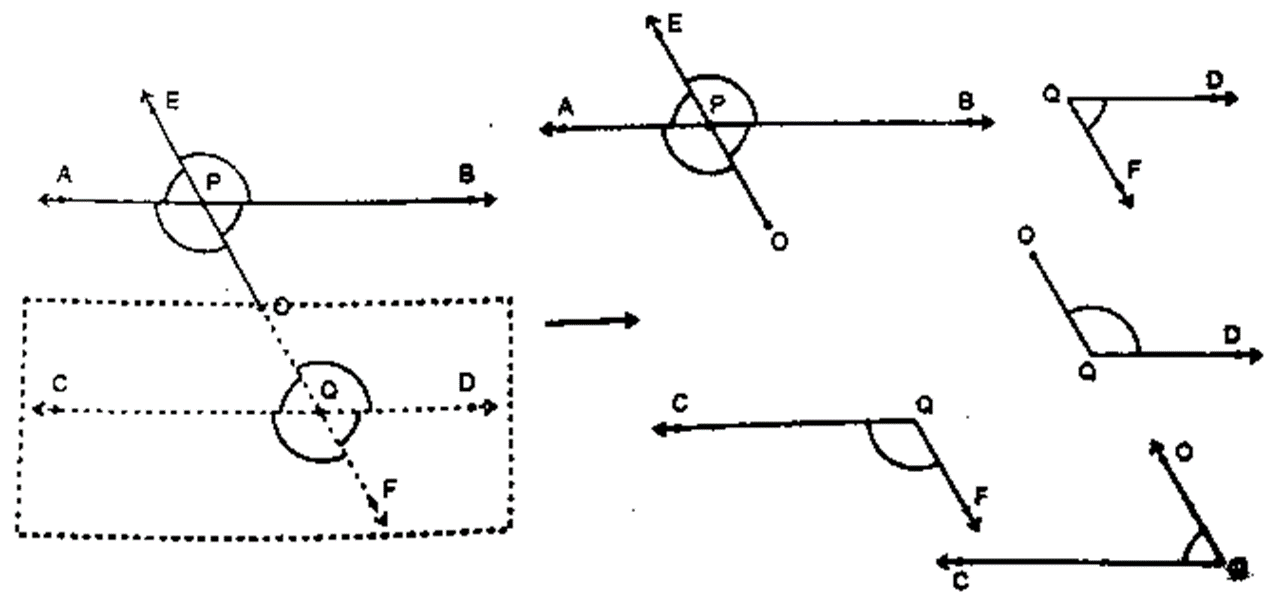
2. Cut the angular regions ∠OQC, ∠ OQD ∠ OPA and ∠ OPB.
3. Draw a line segment and take a point X on it. Paste the angular cut out OQD such that Q coincides with X and QD falls along the Straight line.
Now, paste the angular cut out OPB such that P coincides with X and PO falls along QO.
4. Draw another line segment and take a point Y on it. Paste the angular cut out OQC such that Q coincides with Y and QC falls along the straight line. Now, paste the angular cut out OPA such that P coincides with Y and PO falls along QO.
Observations:
In figure 1, AB || CD and EF is a transversal.
So, (∠ APO, ∠ CQO) and (∠ BPO, ∠ DRO) are two pairs of interior angles on the same side of the transversal.
2. In figure 3, BD is a straight line. So, ∠ BXD = 180 °or
∠ BPO + ∠ DRO = 180 °
3. In figure 4, AC is a straight line.
So, ∠ AYC = 180 °or ∠ APO + ∠ CQO = 180 °
Conclusion:
From the above activity, we can say that if two parallel lines are cut by a transversal, then each pair of interior angles on the same side of the transversal are supplementary.