Class 08 Activity – Data handling

Objective: 

To collect, classify and represent data as a histogram.

Materials Required: 

White sheets of paper, squared paper, colour pencils, a pair of scissors, glue stick, geometry box, etc.

Procedure:

1. For every student of your class (including yourself), find the number of hours he/ she spent in watching

 T.V. on the previous Sunday. The data may be recorded in the tabular form as shown below:

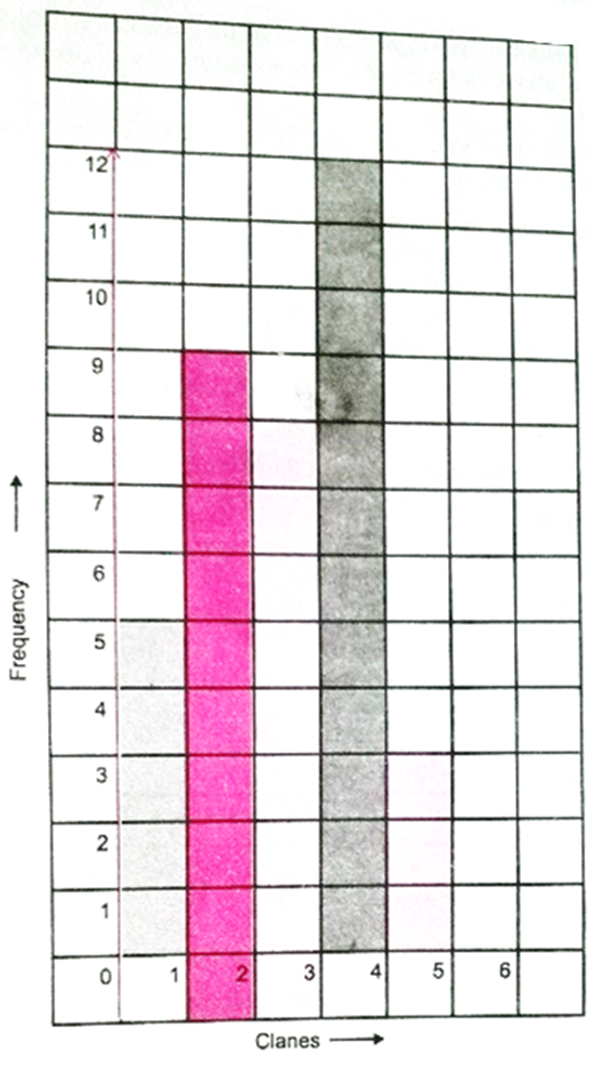
2. Now, draw a histogram on a squared paper representing the class intervals along the horizontal axis and the frequency along the vertical axis as shown below.

Observations:

The bar corresponding to the class 3-4 is longest, So, maximum number of students of your class spent 3 to 4 hours in watching T.V.

2. The bar corresponding to the class 4-5 is shortest. So, minimum number of students of your class spent 4 to 5 hours in watching T.V.

3. Length of the bar corresponding to the class 0-1 = 5

Length of the bar corresponding to the class 1-2 = 9

Length of the bar corresponding to the class 2-3 = 8

Length of the bar corresponding to the class 3-4 = 12

Length of the bar corresponding to the class 4-5 = 3

      Total = 37

Thus, there are 37 students in your class.

4. The number of students who spent less than 3 hours in watching T.V.= 5 + 9 + 8 = 225. 

The number of students who spent 3 or more than 3 hours in watching T.V. = 12 + 3 = 15

Note: The data given above is for your comprehension. The students must do the activity and collect the data.

Do Yourself:

 Do a survey of your class and collect the data from every student of your class(including yourself) to find the number of minutes he/ she spent in playing any outdoor game.

Represent the collected data in the form of a histogram.

 Class 08 Activity – Surface Area 

Objective: 

To Verify the formula for area of a rhombus. Or to verify the following formula: Area of rhombus = 1/2 x product of its diagonals. 

Materials Required:

 gluestick,  Squared paper,  white sheet of paper, colour pencils, a pair of scissors, etc.,

Procedure: 

1. On a squared paper, draw a rhombus ABCD. Join its diagonals AC and BD, which. Intersect each other at o. Colour the four triangles so obtained using different colours.

2. Using a pair of scissors, cut out the four triangles. The cut outs so obtained are four congruent right triangular cut outs. Let the sides forming the right angle of each cut be x and y.

3. Arrange the four triangular cut-outs to form a rectangle as shown below.

Observations: 

Figure 3 is a rectangle of sides (x + x) and y or 2x and y.

So, area of this rectangle 

= 2x x y 

= 1/2 x 2x x 2y

= 1/2 x BD X AC

 [ From figure 1, 2x = BD and 2y = AC]

But, area of rectangle in figure 3 = area of rhombus (ABCD) in figure.

Or area of rhombus ABCD = 1/2 x BD X AC = 1/2 x product of its diagonals.

Conclusion: 

From the above activity, it is verified that : 

Area of a rhombus =1/2 x product of its diagonals.

 Class 08 Activity – Surface Area of a cube and cuboid

Objective: 

To verify the formula for surface area of a cube and a cuboid. Or to verify the following formulae

Surface area of a cube = 6 (side)2.

Surface area of a cuboid= 2 (length x breadth + breadth x height + height x length)

Materials Required: 

Thick sheets of paper, a pair of scissors, sello tape, geometry box, etc.

procedure: 

(a) Cube:

On a thick sheet of paper, draw a net of a cube., as shown below. It consists of six identical squares. Using a pair of scissors, cut it out.

2. Fold the net along the dotted lines and use sellotape to get a cuboid of 

edge 3 cm.

(b) Cuboid:

On a thick sheet of paper, draw the net of a cuboid as shown below. It consists of 6 rectangles. Using a pair of scissors cut it out.

2. Fold the net and use sellotape to form a cuboid of dimensions 

5 cm x 4 cm x 2 cm.

Observations:

Surface area of the cube obtained in figure 2 is equal to the sum of the areas of all the six squares in fig. 

Side of each square = 3 cm

So, area of 1 square = 32 sq cm.

 Area of 6 squares = 6 x 32 sq cm.

Or surface area of the cube in fig = 6 x 32 sq.cm. 

= 6 x (edge)2  sq. units.

2. Surface area of the cuboid in figure is equal to the sum of the areas of all the six rectangles in fig. Figure consists of :

2 rectangles of dimensions 5 cm x 4 cm.

2 rectangles of dimensions 4 cm x 2 cm and

2 rectangles of dimensions 2 cm x 5 cm.

So, sum of the areas of all the rectangles in figure 

= [2 (5 x 4) + 2 (4 x 2) + (2 x 5)] sq cm.

= 2 [(5 x 4) + (4 x 2) + (2 x 5)] sq cm.

Or surface area of the cuboid in figure 

= 2 [(5 x 4) + (4 x 2) + (2 x 5)] sq cm.

= 2 [length x breadth + breadth x height + height x length] sq units.

Conclusion : 

From the above activity, it is verified that : 

Total surface area of a cube = 6(edge)2

(b) Total surface area of a cuboid 

= 2 [length x breadth + breadth x height + height x length] sq units.

 Class 08 Activity – Area of Trapezium

Objective: 

To verify the formula for area of a trapezium. Or to verify the following formula Area of a trapezium = 1/2 sum of the parallel sides x distance between them.

Materials Required: 

Squared paper, a pair of scissors, colour pencils, geometry box, etc.

Procedure: 

1. On a squared paper, draw a trapezium ABCD in which AB || CD and AB = 8 cm, CD = 4 cm and distance between them is 5 cm. 

Using a pair of scissors, cut it out. Colour it green. 

2. On another squared sheet draw one more copy of the parallelogram ABCD. Cut it out and colour it red.

3. Take a white sheet of paper and paste the green coloured trapezium ABCD on it. Paste the red coloured trapezium ABCD next to the green coloured trapezium such that A falls at D and AD falls along DA as shown below.

Observations:

In figure, we observe that the resulting shape is a parallelogram as its one pair of opposite sides is parallel and equal, each equal to (8 + 4) cm.

2. The parallelogram in figure is made up of two congruent trapeziums ABCD.

So, area of trapezium ABCD 

= 1/2 x area of parallelogram in figure 

= 1/2x base x height

= 1/2 x (8 + 4) x 5 cm

= 1/2 x sum of parallel sides x distance between them.

Conclusion: 

From the above activity, it is verified that:

Area of a trapezium = 1/2 x sum of parallel sides x distance between them.

Do Yourself: Verify the formula for area of a trapezium by drawing three different trapeziums on squared papers.