QUESTION BANK CLASS 8 DATA HANDLING

  QUESTION BANK  CLASS 8 DATA HANDLING

The information collected in all such cases is called data.

A Pictograph: Pictorial representation of data using symbols.

A bar graph: A display of information using bars of uniform width, their heights being proportional to the respective values.

Double Bar Graph: A bar graph showing two sets of data simultaneously. It is useful for the comparison of the data. 

A circle graph shows the relationship between a whole and its parts. Here, the whole circle is divided into sectors. The size of each sector is proportional to the activity or information it represents.

A circle graph is also called a pie chart. 

Each outcome of an experiment or a collection of outcomes make an event. For example in the experiment of tossing a coin, getting a Head is an event and getting a Tail is also an event.

In case of throwing a die, getting each of the outcomes 1, 2, 3, 4, 5 or 6 is an event.  

1. In order to draw meaningful inferences from any data, we need to organise the data systematically. 

2. Data can also be presented using circle graph or pie chart. A circle graph shows the relationship between a whole and its part

3. There are certain experiments whose outcomes have an equal chance of occurring. 

4. A random experiment is one whose outcome cannot be predicted exactly in advance. 

5. Outcomes of an experiment are equally likely if each has the same chance of occurring. 

6. Probability of an event = $\frac{Number of outcomes that make an event}{Total number of outcomes of the experiment}$ , when the outcomes are equally likely. 

7. One or more outcomes of an experiment make an event. 

8. Chances and probability are related to real life.

EXAMPLE

A bag has 4 red balls and 2 yellow balls. (The balls are identical in all respects other than colour). A ball is drawn from the bag without looking into the bag. What is probability of getting a red ball? Is it more or less than getting a yellow ball?

Adjoining pie chart (Fig 4.4) gives the expenditure (in percentage) on various items and savings of a family during a month. (i) On which item, the expenditure was maximum? (ii) Expenditure on which item is equal to the total savings of the family? (iii) If the monthly savings of the family is ` 3000, what is the monthly expenditure on clothes?

On a particular day, the sales (in rupees) of different items of a baker’s shop are given below. 

ordinary bread : 320 

fruit bread : 80 

cakes and pastries : 160

biscuits : 120 

others : 40 

Total : 720 

Draw a pie chart for this data. 

EXERCISE 4.1 

1. A survey was made to find the type of music that a certain group of young people liked in a city. Adjoining pie chart shows the findings of this survey. From this pie chart answer the following: 

(i) If 20 people liked classical music, how many young people were surveyed? 

(ii) Which type of music is liked by the maximum number of people? 

(iii) If a cassette company were to make 1000 CD’s, how many of each type would they make? 

2. A group of 360 people were asked to vote for their favourite season from the three seasons rainy, winter and summer. 

(i) Which season got the most votes? 

(ii) Find the central angle of each sector. 

(iii) Draw a pie chart to show this information. 

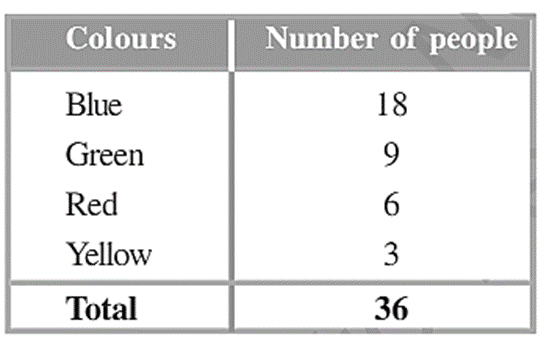
3. Draw a pie chart showing the following information. The table shows the colours preferred by a group of people. 

Colours Number of people 

Blue 18 

Green 9 

Red 6 

Yellow 3 

Total 36 

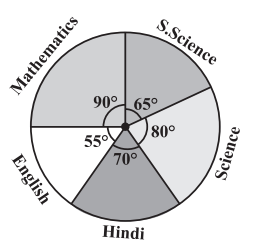
4. The adjoining pie chart gives the marks scored in an examination by a student in Hindi, English, Mathematics, Social Science and Science. If the total marks obtained by the students were 540, answer the following questions. 

(i) In which subject did the student score 105 marks?
(Hint: for 540 marks, the central angle = 360°. So, for 105 marks, what is the central angle?) 

(ii) How many more marks were obtained by the student in Mathematics than in Hindi? 

(iii) Examine whether the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi. (Hint: Just study the central angles)

5. The number of students in a hostel, speaking different languages is given below. Display the data in a pie chart.

Language Hindi English Marathi Tamil Bengali Total 

Number of students  40 12 9 7 4 72 

EXERCISE 4.2 

1. List the outcomes you can see in these experiments. (a) Spinning a wheel (b) Tossing two coins together 

2. When a die is thrown, list the outcomes of an event of getting (i) (a) a prime number (b) not a prime number. (ii) (a) a number greater than 5 (b) a number not greater than 5. 

3. Find the. (a) Probability of the pointer stopping on D in (Question 1-(a))? 

(b) Probability of getting an ace from a well shuffled deck of 52 playing cards? 

(c) Probability of getting a red apple. (See figure below) 

4. Numbers 1 to 10 are written on ten separate slips (one number on one slip), kept in a box and mixed well. One slip is chosen from the box without looking into it. 

What is the probability of . 

(i) getting a number 6? 

(ii) getting a number less than 6? 

(iii) getting a number greater than 6? 

(iv) getting a 1-digit number? 

5. If you have a spinning wheel with 3 green sectors, 1 blue sector and 1 red sector, what is the probability of getting a green sector? What is the probability of getting a non blue sector? 

6. Find the probabilities of the events given in Question 2.

QUESTION BANK CLASS 8 UNDERSTANDING QUADRILATERALS

  QUESTION BANK  CLASS 8 UNDERSTANDING QUADRILATERALS

• A simple closed curve made up of only line segments is called a polygon.
• Polygons that are convex have no portions of their diagonals in their exteriors or any line segment joining any two different points, in the interior of the polygon, lies wholly in the interior of it
• A regular polygon is both ‘equiangular’ and ‘equilateral’. For example, a square has sides of equal length and angles of equal measure. Hence it is a regular polygon. 
• A rectangle is equiangular but not equilateral.
• 
  
• the sum of the measures of the external angles of any polygon is 360°
• Trapezium is a quadrilateral with a pair of parallel sides
• Kite is a special type of a quadrilateral. The sides with the same markings in each figure are equal. For example AB = AD and BC = CD.
• A kite has 4 sides (It is a quadrilateral). (ii) There are exactly two distinct consecutive pairs of sides of equal length.
• A parallelogram is a quadrilateral. As the name suggests, it has something to do with parallel lines.
• A parallelogram is a quadrilateral whose opposite sides are parallel.
• There are four sides and four angles in a parallelogram.  
• The opposite sides of a parallelogram are of equal length.
• The opposite angles of a parallelogram are of equal measure.
•  The diagonals of a parallelogram, in general, are not of equal length.
• The diagonals of a parallelogram bisect each other.
• A rhombus is a quadrilateral with sides of equal length. Since the opposite sides of a rhombus have the same length, it is also a parallelogram. So, a rhombus has all the properties of a parallelogram and also that of a kite.
• The diagonals of a rhombus are perpendicular bisectors of one another.
• A rectangle is a parallelogram with equal angles.
• a rectangle is a parallelogram in which every angle is a right angle. Being a parallelogram, the rectangle has opposite sides of equal length and its diagonals bisect each other.
• The diagonals of a rectangle are of equal length.
• In a rectangle the diagonals, besides being equal in length bisect each other.
• A square is a rectangle with equal sides.
• In a square the diagonals. 
• (i) bisect one another (square being a parallelogram) 
• (ii) are of equal length (square being a rectangle) and 
• (iii) are perpendicular to one another.
• The diagonals of a square are perpendicular bisectors of each other 

POINTS TO REMEMBER

Parallelogram: 

• A quadrilateral with each pair of opposite sides parallel.
• (1) Opposite sides are equal. (2) Opposite angles are equal. (3) Diagonals bisect one another.

Rhombus: 

• A parallelogram with sides of equal length.
• (1) All the properties of a parallelogram. (2) Diagonals are perpendicular to each other.

Rectangle: A parallelogram with a right angle

(1) All the properties of a parallelogram. (2) Each of the angles is a right angle. (3) Diagonals are equal.

Square: A rectangle with sides of equal length.

All the properties of a parallelogram, rhombus and a rectangle. 

Kite: A quadrilateral with exactly two pairs of equal consecutive sides

(1) The diagonals are perpendicular to one another (2) One of the diagonals bisects the other. (3) In the figure m∠B = m∠D but m∠A ≠ m∠C.  

EXERCISE 3.1 

• 1. Given here are some figures 

Classify each of them on the basis of the following. (a) Simple curve (b) Simple closed curve (c) Polygon (d) Convex polygon (e) Concave polygon 

• 2. What is a regular polygon? State the name of a regular polygon of (i) 3 sides (ii) 4 sides (iii) 6 sides

EXERCISE 3.2 

• 1. Find x in the following figures. 

• 2. Find the measure of each exterior angle of a regular polygon of (i) 9 sides (ii) 15 sides 
• 3. How many sides does a regular polygon have if the measure of an exterior angle is 24°?
•  4. How many sides does a regular polygon have if each of its interior angles is 165°? 
• 5. (a) Is it possible to have a regular polygon with measure of each exterior angle as 22°? 
• (b) Can it be an interior angle of a regular polygon? Why? 
• 6. (a) What is the minimum interior angle possible for a regular polygon? Why?
•  (b) What is the maximum exterior angle possible for a regular polygon?

EXERCISE 3.3 

1. Given a parallelogram ABCD. Complete each statement along with the definition or property used. (i) AD = ...... (ii) ∠ DCB = ...... (iii) OC = ...... (iv) m ∠DAB + m ∠CDA = ...... 

2. Consider the following parallelograms. Find the values of the unknowns x, y, z.

3. Can a quadrilateral ABCD be a parallelogram if (i) ∠D + ∠B = 180°? (ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm? (iii) ∠A = 70° and ∠C = 65°? 

4. Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure. 

5. The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram. 

6. Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram. 

7. The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them. 

8. The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm) 

9. In the above figure both RISK and CLUE are parallelograms. Find the value of x.

10. Explain how this figure is a trapezium. Which of its two sides are parallel? (Fig) 

11. Find m∠C in Fig, if $\overline{AB}\parallel \overline{DC}$  . 

12. Find the measure of ∠P and ∠S if $\overline{SP}\parallel \overline{RQ}$ in Fig. (If you find m∠R, is there more than one method to find m∠P?)

EXERCISE 3.4 

1. State whether True or False.
(a) All rectangles are squares 

(e) All kites are rhombuses. 

(b) All rhombuses are parallelograms 

(f) All rhombuses are kites. 

(c) All squares are rhombuses and also rectangles 

(g) All parallelograms are trapeziums. 

(d) All squares are not parallelograms. 

(h) All squares are trapeziums. 

2. Identify all the quadrilaterals that have. 

(a) four sides of equal length 

(b) four right angles 

3. Explain how a square is. 

(i) a quadrilateral 

(ii) a parallelogram 

(iii) a rhombus 

(iv) a rectangle 

4. Name the quadrilaterals whose diagonals. 

(i) bisect each other 

(ii) are perpendicular bisectors of each other 

(iii) are equal 

5. Explain why a rectangle is a convex quadrilateral. 

6. ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).

EXAMPLE

• Find the number of sides of a regular polygon whose each exterior angle has a measure of 45°.
• RENT is a rectangle (Fig 3.35). Its diagonals meet at O. Find x, if OR = 2x + 4 and OT = 3x + 1.
• 
  
  
  
• RICE is a rhombus (Fig 3.30). Find x, y, z. Justify your findings.
• 
  
  
  
• In Fig, HELP is a parallelogram. (Lengths are in cms). Given that OE = 4 and HL is 5 more than PE? Find OH.

•  In a parallelogram RING, (Fig 3.22) if m∠R = 70°, find all the other angles

• In Fig, BEST is a parallelogram. Find the values x, y and z.

• Find the perimeter of the parallelogram PQRS 
  
  
  
• 
  

• Find measure x in Fig.

QUESTION BANK CLASS 8 LINEAR EQUATIONS WITH ONE VARIABLES

 QUESTION BANK  CLASS 8 LINEAR EQUATIONS WITH ONE VARIABLES

•  An algebraic equation is an equality involving variables. It has an equality sign. The expression on the left of the equality sign is the Left Hand Side (LHS). The expression on the right of the equality sign is the Right Hand Side (RHS).
• In an equation the values of the expressions on the LHS and RHS are equal. This happens to be true only for certain values of the variable. These values are the solutions of the equation. 

EXAMPLE

• Solve 2x – 3 = x + 2
• 
  
  
  

EXERCISE 2.1

 Solve the following equations and check your results

1. 3x = 2x + 18 

2. 5t – 3 = 3t – 5 

3. 5x + 9 = 5 + 3x 

4. 4z + 3 = 6 + 2z 

5. 2x – 1 = 14 – x 

6. 8x + 4 = 3 (x – 1) + 7

EXERCISE 2.2 

Solve the following linear equations. 

Simplify and solve the following linear equations. 

7. 3(t – 3) = 5(2t + 1) 

8. 15(y – 4) –2(y – 9) + 5(y + 6) = 0 

9. 3(5z – 7) – 2(9z – 11) = 4(8z – 13) – 17 

10. 0.25(4f – 3) = 0.05(10f – 9) 

POINTS TO REMEMBER

1. An algebraic equation is an equality involving variables. It says that the value of the expression on one side of the equality sign is equal to the value of the expression on the other side. 

2. The equations we study in Classes VI, VII and VIII are linear equations in one variable. In such equations, the expressions which form the equation contain only one variable. Further, the equations are linear, i.e., the highest power of the variable appearing in the equation is 1. 

3. An equation may have linear expressions on both sides. Equations that we studied in Classes VI and VII had just a number on one side of the equation. 

4. Just as numbers, variables can, also, be transposed from one side of the equation to the other. 

5. Occasionally, the expressions forming equations have to be simplified before we can solve them by usual methods. Some equations may not even be linear to begin with, but they can be brought to a linear form by multiplying both sides of the equation by a suitable expression. 

6. The utility of linear equations is in their diverse applications; different problems on numbers, ages, perimeters, combination of currency notes, and so on can be solved using linear equations.

QUESTION BANK CLASS 8 RATIONAL NUMBERS

  QUESTION BANK  CLASS 8 RATIONAL NUMBERS

EXERCISE 1.1

 1. Name the property under multiplication used in each of the following

2. Tell what property allows you to compute

3. The product of two rational numbers is always a ___.

POINTS TO REMEMBER

• A number which can be written in the form p q , where p and q are integers and q ≠ 0 is called a rational number
• rational numbers are closed under addition. That is, for any two rational numbers a and b, a + b is also a rational number.
• rational numbers are closed under subtraction. That is, for any two rational numbers a and b, a – b is also a rational number.
• rational numbers are closed under multiplication. That is, for any two rational numbers a and b, a × b is also a rational number.
• for any rational number a, a ÷ 0 is not defined. So rational numbers are not closed under division.
• two rational numbers can be added in any order. We say that addition is commutative for rational numbers. That is, for any two rational numbers a and b, a + b = b + a.
• subtraction is not commutative for integers and integers are also rational numbers. So, subtraction will not be commutative for rational numbers too.
• multiplication is commutative for rational numbers. In general, a × b = b × a for any two rational numbers a and b.
• division is not commutative for rational numbers.
• addition is associative for rational numbers. That is, for any three rational numbers a, b and c, a + (b + c) = (a + b) + c.
• Subtraction is not associative for rational numbers.
• multiplication is associative for rational numbers. That is for any three rational numbers a, b and c, a × (b × c) = (a × b) × c.
• division is not associative for rational numbers.
• Zero is called the identity for the addition of rational numbers. It is the additive identity for integers and whole numbers as well.
• a × 1 = 1 × a = a for any rational number a 
• 1 is the multiplicative identity for rational numbers.
• Distributivity of Multiplication over Addition and Subtraction. For all rational numbers a, b and c, a (b + c) = ab + ac a (b – c) = ab – ac

1. Rational numbers are closed under the operations of addition, subtraction and multiplication. 

2. The operations addition and multiplication are (i) commutative for rational numbers. (ii) associative for rational numbers. 

3. The rational number 0 is the additive identity for rational numbers. 

4. The rational number 1 is the multiplicative identity for rational numbers. 

5. Distributivity of rational numbers: 

For all rational numbers a, b and c, a(b + c) = ab + ac and a(b – c) = ab – ac 

6. Between any two given rational numbers there are countless rational numbers. 

The idea of mean helps us to find rational numbers between two rational numbers.