QUESTION BANK CLASS 8 LINEAR EQUATIONS WITH ONE VARIABLES
- An algebraic equation is an equality involving variables. It has an equality sign. The expression on the left of the equality sign is the Left Hand Side (LHS). The expression on the right of the equality sign is the Right Hand Side (RHS).
- In an equation the values of the expressions on the LHS and RHS are equal. This happens to be true only for certain values of the variable. These values are the solutions of the equation.
EXAMPLE
- Solve 2x – 3 = x + 2
EXERCISE 2.1
Solve the following equations and check your results
1. 3x = 2x + 18
2. 5t – 3 = 3t – 5
3. 5x + 9 = 5 + 3x
4. 4z + 3 = 6 + 2z
5. 2x – 1 = 14 – x
6. 8x + 4 = 3 (x – 1) + 7
EXERCISE 2.2
Solve the following linear equations.
Simplify and solve the following linear equations.
7. 3(t – 3) = 5(2t + 1)
8. 15(y – 4) –2(y – 9) + 5(y + 6) = 0
9. 3(5z – 7) – 2(9z – 11) = 4(8z – 13) – 17
10. 0.25(4f – 3) = 0.05(10f – 9)
POINTS TO REMEMBER
1. An algebraic equation is an equality involving variables. It says that the value of the expression on
one side of the equality sign is equal to the value of the expression on the other side.
2. The equations we study in Classes VI, VII and VIII are linear equations in one variable. In such
equations, the expressions which form the equation contain only one variable. Further, the equations
are linear, i.e., the highest power of the variable appearing in the equation is 1.
3. An equation may have linear expressions on both sides. Equations that we studied in Classes VI
and VII had just a number on one side of the equation.
4. Just as numbers, variables can, also, be transposed from one side of the equation to the other.
5. Occasionally, the expressions forming equations have to be simplified before we can solve them
by usual methods. Some equations may not even be linear to begin with, but they can be brought
to a linear form by multiplying both sides of the equation by a suitable expression.
6. The utility of linear equations is in their diverse applications; different problems on numbers, ages,
perimeters, combination of currency notes, and so on can be solved using linear equations.



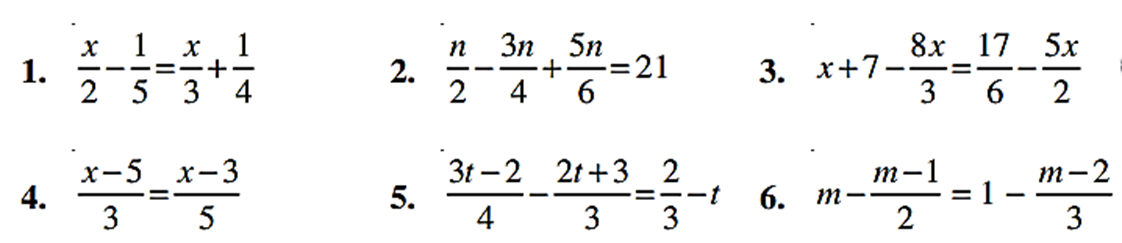
No comments:
Post a Comment