Class 8 NCERT bridge course Answers Activity W 4.6 A fractal

 Activity W 4.6 A fractal

Objective:

 This activity will help students to: 

• Understand the concept of fractals.

• Build a simple fractal (Sierpinski Triangle   or Koch Snowflake) using repeated patterns.

Materials Required: 

Paper, markers, ruler (optional), printouts of basic geometric shapes (triangles, squares, etc.). 

A fractal is a shape or pattern that repeats itself no matter how much you zoom into it. 

Procedure

 Guide students to build fractals step-by-step. 

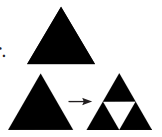
1. Draw a large equilateral triangle on your paper. 

2. Find the midpoints of each side and join them. Remove the middle triangle so obtained. 

It will look as shown—

 3. Again, join the midpoints of each of the sides of the three shaded triangles. 

Remove the three triangles so obtained. It will look like

4. Ask the students to continue the process for at least two more times. 

Take sufficiently large paper or cardboard for this purpose. 

Reflection

 Ask the students to describe the final structure they obtain. 

ANSWER:

The final structure looks like a big triangle made up of smaller and smaller triangles.

Does the final one looks like a big triangle made up of smaller triangles, and if we zoom in,?

ANSWER:

Yes! If we zoom in, the same pattern keeps repeating — this is the main property of a fractal.

 do we see the same pattern inside? This is a fractal. 

ANSWER:

• A fractal shows self-similarity: no matter how much you zoom in or out, the shape looks the same.

• Pattern Observation:

  • Number of triangles increases at every step:

    • Step 1: 1 large triangle.

    • Step 2: 3 shaded triangles.

    • Step 3: 9 smaller shaded triangles.

    • Step 4: 27 even smaller shaded triangles.

  The number of triangles follows this pattern:
  Number of shaded triangles = 3ⁿ (n = step number)

Extension

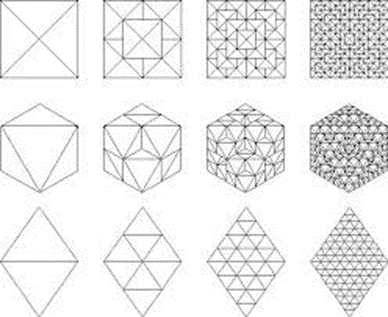
 1. Students may try this for different shapes, such as square, rectangle, parallelogram or any other shape of their choice. 

1. Try this fractal pattern with other shapes like:

   • Squares (creates a Sierpinski Carpet),

   • Rectangles,

   • Parallelograms,

   • Hexagons.

Squares – Sierpinski Carpet

• Step 1: Start with one large square.

• Step 2: Divide the square into 9 smaller squares (like a tic-tac-toe grid).

• Remove the middle square.

• Step 3: For each remaining square, repeat the same process: divide into 9 parts, remove the middle one.

• Keep repeating!

👉 Pattern:

• Number of remaining squares grows as 8ⁿ (n = step number).

• Creates a flat, grid-like fractal called the Sierpinski Carpet.

Rectangles

• Step 1: Start with a rectangle.

• Step 2: Divide it into equal smaller rectangles (4, 6, 8 parts or more, depending on shape).

• Remove a central part or selected parts.

• Repeat the same for the remaining rectangles.

Pattern:

• You will get a rectangular fractal where the shape keeps splitting into smaller rectangles, showing self-similarity.

Parallelograms

• Step 1: Start with a parallelogram.

• Step 2: Divide it into smaller, identical parallelograms.

• Remove one or more central parts.

• Repeat the process for each remaining parallelogram.

Pattern:

• The structure will look like a stretched or skewed version of the square fractal, but still self-similar and recursive.

Hexagons

• Step 1: Start with a regular hexagon.

• Step 2: Divide the hexagon into 7 smaller hexagons (1 central + 6 surrounding).

• Remove the central hexagon.

• Repeat the process for each remaining hexagon.

Pattern:

• A repeating honeycomb-like fractal — looks similar to snowflake patterns or beehives!

• The edges form increasingly complex, yet balanced, hexagon-based designs.

No matter the shape — square, rectangle, parallelogram, or hexagon — when you:

1. Divide,

2. Remove parts,

3. Repeat the process...

...you create a fractal: a never-ending, self-similar, and geometric pattern.

2. Students may be asked to associate numbers with each shape. 

Say, number of triangles obtained in each step or the number sides on outer edges in each step (3, 6, ...).

 They need to find a pattern.

Pattern in Outer Edges

• As you remove triangles, the number of sides or edges grows.
• For each step, the outer shape becomes more detailed but still follows a predictable mathematical pattern.

Sierpinski Triangle

• Number of Triangles at Each Step:

  Step	Triangles Formed
  0 (Start)	1
  1	3
  2	9
  3	27
  4	81

  Pattern:
  Number of triangles = 3ⁿ (where n = step number)

   Outer Edges (Visible Triangle Sides):

  Step	Outer Edges
  0	3
  1	6
  2	12
  3	24

  Pattern:
  Outer triangle sides double each step: 3 × 2ⁿ

  Sierpinski Carpet (Square Fractal)

   Number of Squares at Each Step:

  Step	Squares Remaining
  0	1
  1	8
  2	64
  3	512

  Pattern:
  Number of squares = 8ⁿ

   Outer Edges:

  Step	Squares on One Side	Total Outer Sides
  0	1	4
  1	3	12
  2	9	36
  3	27	108

  Pattern:

  • Each side is split into 3ⁿ parts.

  • Total outer sides = 4 × 3ⁿ

  Parallelogram Fractal (Custom logic – similar to square)

  If we divide into 4 parts (2×2 layout) and remove the middle one:

   Number of Parallelograms:

  Step	Shapes
  0	1
  1	3
  2	9
  3	27

  Pattern:
  Just like triangle: 3ⁿ

  Hexagon Fractal

  (Similar to honeycomb — 7 small hexagons, remove the center)

  Number of Hexagons:

  Step	Hexagons Remaining
  0	1
  1	6
  2	36
  3	216

  Pattern:
  Number of hexagons = 6ⁿ

  Summary Table:

  Shape	Shapes per Step	Pattern	Outer Sides Pattern
  Triangle	3ⁿ triangles	Exponential	3 × 2ⁿ
  Square	8ⁿ squares	Exponential	4 × 3ⁿ
  Parallelogram	3ⁿ parallelograms	Exponential	Similar to triangle logic
  Hexagon	6ⁿ hexagons	Exponential	Grows like a honeycomb

• 
  

Conclusion:

A fractal is a fascinating geometric figure where the same pattern repeats itself at every scale. 

The Sierpinski Triangle is a perfect example of this, and by exploring other shapes, we can discover many more fractals in nature and mathematics.