Class – 6 CH-7 FRACTIONS

MATHS NCERT SOLUTIONS

Exercise 7.1

Question 1:

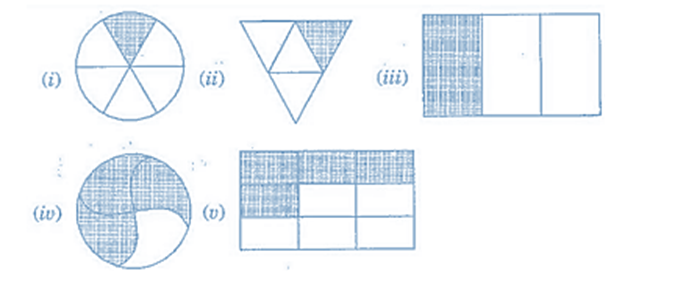
Write the fraction representing the shaded portion:

Solution 1:

(i) 2/4 = ½

(ii) 8/9

(iii) 4/8

(iv) 1/4

(v) 3/7

(vi) 3/12

(vii) 10/10 =1

(viii) 4/9

(ix) 4/8

(x) 1/2

Question 2:

Colour the part according to the given fraction:

Solution 2:

Question 3:

Identify the error, if any?

Solution 3:

All the figures are not equally divided. For making fractions, it is necessary that figure is to be divided in equal parts.

Question 4:

What fraction of a day is 8 hours?

Solution 4:

Since, 1 day = 24 hours.

Therefore, the fraction of 8 hours = 8/24 = 1/3

Question 5:

What fraction of an hour is 40 minutes?

Solution 5:

Since, 1 hour = 60 minutes.

Therefore, the fraction of 40 minutes = 40/60 =2/3

Question 6:

Arya, Abhimanyu and Vivek shared lunch. Arya has brought two sandwiches, one made of vegetable and one of jam. The other two boys forgot to bring their lunch. Arya agreed to share his sandwiches so that each person will have an equal share of each sandwich.

(a) How can Arya divide his sandwiches so that each person has an equal share?

(b) What part of a sandwich will each boy receive?

Solution 6:

(a) Arya will divide each sandwich into three equal parts and give one part of each sandwich to each one of them.

(b) 1 

3 3

Question 7:

Kanchan dyes dresses. She had to dye 30 dresses. She has so far finished 20 dresses. What fraction of dresses has she finished? Solution 7:

Total number of dresses = 30

Work finished = 20

20 2

Fraction of finished work = 

30 3

Question 8: Write the natural numbers from 2 to 12. What fraction of them are prime numbers?

Solution 8:

Natural numbers from 2 to 12: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 Prime numbers from 2 to 12: 2, 3, 5, 7, 11

Hence, fraction of prime numbers =

Question 9:

Write the natural numbers from 102 to 113. What fraction of them are prime numbers?

Solution 9:

Natural numbers from 102 to 113:

102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113

Prime numbers from 102 to 113:

103, 107, 109, 113

4 1

Hence fraction of prime numbers = 

12 3

Question 10:

What fraction of these circles have ‘X’s in them?

Solution 10:

Total number of circles = 8 and number of circles having ‘X’ = 4

Hence, the fraction =

Question 11:

Kristin received a CD player for her birthday. She bought 3 CDs and received 5 others as gifts. What fraction of her total CDs did she buy and what fraction did she receive as gifts?

Solution 11:

Total number of CDs = 3 + 5 = 8

Number of CDs purchased = 3

Fraction of CDs purchased =

Fraction of CDs received as gifts =

Exercise 7.2

Question 1:

Draw number lines and locate the points on them:

1 1 3 4

(a) , , ,

2 4 4 4

1 2 3 7

(b) , , ,

8 8 8 8

2 3 8 4

5 5 5 5

Solution 1:

(a)

(b)

(c)

Question 2:

Express the following fractions as mixed fractions:

(a)

(b)

(c)

(d)

(e)

(f)

Solution 2:

(a) 3 20

18

2 (b) 2

5 11

10

20 2   6

3 3 11 1   2

5 5

7 17

14

3 (d) 5

5 28

25

17 3   2

7 7 28 3   5

5 5

(e) 3

6 19

18

1 (f) 3

9 35

27

19 1   3 6 6 35 8   3

9 9

Question 3:

Express the following as improper fractions:

(a) 7

(b) 5

(d) 10

(e) 9

(f) 8

Solution 3:

3 7 4 3  28 3 31

(a) 7   

4 4 4 4

6 5 7 6  35 6 41

(b) 5   

7 7 7 7

5 2 6 5  12 5 17

6 6 6 6

3 10 5 3  50 3 53

(d) 10   

5 5 5 5

3 9 7 3  63 3 66

(e) 9   

7 7 7 7

4 8 9 4  72 4 76

(f) 8   

9 9 9 9

Exercise 7.3

Question 1:

Write the fractions. Are all these fractions equivalent:

Yes, all of these fractions are equivalent.

4 3 2 1 6

(b) , , , ,

12 9 6 3 15

No, these fractions are not equivalent.

Question 2:

Write the fraction and pair up the equivalent fractions to each row:

Solution 2:

(a) (ii) 

(b)  (iv) 

612

918

(d)  (v) 

816

(e) (iii) 

Question 3:

Replace in each of the following by the correct number:

2 8 5 10 3

(a)  (b)  (c) 

785 20

45 15 18

(d)  (e) 

6024 4

Solution 3:

(a) (b) (c)

45 45 3 15 (d)  

60 60 3 18 18 6 3

(e)  

24 24 6 4

Question 4:

Find the equivalent fraction of having:

(a) denominator 20 (b) numerator 9

Solution 4:

(a) (b)

Question 5:

Find the equivalent fraction of with:

(a) numerator 9 Solution 5: (b) denominator 4

36 36 4 9 36 36 12 3

(a)   (b)   48 48 4 12 48 48 12 4

Question 6:

Check whether the given fraction are equivalent:

5 30 3 12

(a) , (b) ,

9 54 10 50

Solution 6: 7 5

13 11

5 30 5 6 30 (a) , = , =

9 54 9 6 54 30 30 ,

54 54

Therefore, are equivalent.

3 12 3 5 12

(b) , = , =

10 50 10 5 50

3 12

Therefore, , are not equivalent.

10 50 15 12

50 50

7 5 7 11

13 11 13 11 11 13  77 65

= ,

143 143

7 5

Therefore, , are not equivalent fraction.

13 11

Question 7:

Reduce the following fractions to simplest form:

(a) (b) (c) (d) (e)

Solution 7:

48 2  2 2 2 3150 3  5 10 5 (a)  (b)  

60 2 3  10 2

98 13

(e)  

28 2 2  7 4

Question 8:

Ramesh had 20 pencils, Sheelu had 50 pencils and Jamaal had 80 pencils. After 4 months, Ramesh used up 10 pencils, Sheelu used up 25 pencils and Jamaal used up 40 pencils. What fraction did each use up? Check is each has used up an equal fraction of her/his pencils?

Solution 8:

Ramesh: Total pencils = 20

Pencils used = 10

10 1

Fraction = 

20 2

Sheelu: Total pencils = 50

Pencils used = 25

25 1

Fraction = 

50 2

Jamaal: Total pencils = 80

Pencils used = 40

40 1

Fraction = 

80 2

Since, all of them used half of their pencils, therefore each one used up equal fraction of pencils.

Question 9:

Match the equivalent fractions and write two more for each:

(i) (a)

(ii) (b)

(iii) (c)

(iv) (d)

(v) (e)

Solution 9:

250 5 10 15

(i)  , , (d)

400 8 16 24

180 9 18 27

(ii)  , , (e)

200 10 20 30

660 2 4 6 (iii)  , , (a)

990 3 6 9

180 1 2 3 (iv)  , , (c)

360 2 4 6

220 2 4 6 (v)  , , (b)

550 5 10 15

Exercise 7.4

Question 1:

Write shaded portion as fraction. Arrange them in ascending and descending order using correct sign ‘<’, ‘>’, ‘=’ between the fractions:

given:

6 6 6 6 6 6 6

Solution 1:

3 6 4 1

(a) , , ,

8 8 8 8

Ascending order: 1 3 4 6

   8 8 8 8

Descending order:

8 4 3 6

(b) , , ,

9 9 9 9 6 4 3 1

   8 8 8 8

Ascending order: 3 4 6 8    9 9 9 9

Descending order: 8 6 4 3    9 9 9 9

52 3 16 85

, 0, ,

Question 2:

Compare the fractions and put an appropriate sign:

35 (a)

11 (b)

45 (c)

(d)

Solution 2:

3 5 (a) 

6 6

1 1 (b) 

7 4

4 5 (c) 

5 5

3 3

(d) 

5 7

Question 3: Make five more each pairs and put appropriate signs.

Solution 3:

9 6 (a) 

10 10

1 1 (b) 

3 6

1 1

8 5

7 11

(d) 

8 8

11 9 (e)  13 13

Question 4:

Look at the figures and write ‘<’ or ‘>’ between the given pairs of fractions:

63 55

(d) (e)

63 65

Make five more such problems and solve them with your friends. Solution 4:

1 1 3 2 2 2

(b)  (b)  (c) 

6 3 4 6 3 4

6 3 5 5

(d)  (e) 

6 3 6 5

Five more such problems:

13 (a)

23 (b)

34 (c)

52 (d)

(e)

Solution:

1 3

(a) =

2 6 2 3

(b) >

3 5 3 4

4 6

5 2

(d) <

6 2

0 0

(e) =

1 6

Question 5:

How quickly can you do this? Fill a

11 (a) 25 ppropriate sign (<, =, >):

23 (b)

32 (c) 53

32 (d)

36 (e)

73 (f)

12 (g)

64 (h)

105

37 (i)

64 (j)

105

515 (k)

721

Solution 5:

1 1

(a) >

2 5 2 3

(b) =

4 6 3 2

5 3

3 2

(d) >

4 8 3 6

(e) <

5 5 7 3

(f) >

9 9

1 2

(g) =

4 8 6 4

(h) <

10 5 3 7

(i) <

4 8

6 4

(j) <

10 5

5 15

(k) =

7 21

Question 6:

The following fractions represent just three different numbers. Separate them into three groups of equivalent fractions, by changing each one to its simplest form:

(a) (b) (c) (d) (e) (f)

(g) (h) (i) (j) (k) (l)

Solution 6:

23816

(a)  (b)  (c)  (d) 

121550100

10151216

(e)  (f)  (g)  (h) 

60756096

121234 4

(i)  (j)  (k)  (l) 

75721825 25

Equivalent groups:

I group: [(b), (f), (g)]

II group: [(a), (e), (h), (j), (k)]

III group: [(c), (d), (i), (l)]

Question 7:

Find Solutions to the following. Write and indicate how you solved them:

(a) Is equal to ? (b) Is equal to ?

Solution 7:

(a) and

 and [ L.C.M. of 9 and 5 is 45]

25 36 Since, 

45 45

5 4

Therefore, 

9 5

5 16 80

  [ L.C.M. of 16 and 9 is 144]

9 16 144

81 80 Since, 

144 144

9 5

Therefore, 

16 9

(d) and

 [ L.C.M. of 5 and 20 is 100]

80 80 Since, 

100 100

4 16

Therefore, 

5 20

(e) and

 [ L.C.M. of 15 and 30 is 30]

4 4

Since, 

30 30

1 4

Therefore,  15 30

Question 8:

Ila read 25 pages of a book containing 100 pages. Lalita read of the same book. Who read less?

Solution 8:

Ila read 25 pages out of 100 pages.

25 1

Fraction of reading the pages =  th part of book

100 4

Lalita read th part of book = pages

1 2

Since 

4 5

Therefore, Ila read less.

Question 9:

Rafiq exercised for of an hour, while Rohit exercised for of an hour. Who exercised for a longer time?

Solution 9:

Rafiq exercised of an hour.

Rohit exercised of an hour.

3 3

Since 

4 6

Therefore, Rohit exercised for a longer time.

Question 10:

In a class A of 25 students, 20 passed in first class; in another class B of 30 students, 24 passed in first class. In which class was a greater fraction of students getting first class?

Solution 10:

In class A, 20 passed out of 25, i.e., =

In class B, 24 passed out of 30, i.e., =

Hence, each class have same fraction of student getting first class.

Exercise 7.5

Question 1:

Write the fractions appropriately as additions or subtractions:

Solution 1:

1 2 12 3

(a)   

5 5 5 5

5 3 53 2 (b)   

5 5 5 5

2 3 23 5 (c)   

6 6 6 6

Question 2:

Solve:

1 1

(a) 

18 18 8 3

(b) 

15 15 7 5 (c) 

7 7

1 21 (d) 

22 22 12 7 (e) 

15 15 5 3 (f) 

8 8

(g) 1231 33 (h) 14  04 (i) 3



Solution 2:

1 1 1 1 28 3 83 11

(a)     (b)   

18 18 18 1815 15 15 15

7 5 75 2 1 21 121 22

7 7 7 7 22 22 22 22

12 7 127 55 3 8

(e)     (f)   1

15 15 15 158 8 8

    

3 3 3 2 3   

4 4 4 4

12 15 12 15 12

(i) 3      3

5 5 5 5 5

(g) 1 2 3 2 32 1 (h) 1 0 10 1

Question 3:

Shubham painted of the wall space in his room. His sister Madhavi helped and painted

of the wall space. How much did they paint together?

Solution 3:

Fraction of wall painted by Shubham =

Fraction of wall painted by Madhavi =

2 1 2 1 3

Total painting by both of them =    1

3 3 3

Therefore, they painted complete wall.

Question 4:

Fill in the missing fractions:

7 33 5

(a)   (b)  

10 1021 21

6 6

Solution 4: 27 27

3 35 12

(a) (b)

Question 5: Javed was given of a basket of oranges. What fraction of oranges was left in the basket? Solution 5:

Total = 1

Fraction of Orange left = 1

7 5 75 2

=    7 7 7 7

Thus, oranges was left in the basket.

Exercise 7.6

Question 1:

Solve:

2 1 (a) 

3 7 3 7

(b) 

10 15 4 2

9 7 5 1

(d) 

7 3

2 1 (e) 

5 6 4 2

(f) 

5 3 3 1

(g) 

4 3 5 1

(h) 

6 3

2 3 1

(i)  

3 4 2 1 1 1

(j)  

2 3 6 1 2

(k) 1 3

3 3 2 1

(l) 4 3

3 4

16 7 (m)  5 5 4 1

(n) 

3 2

Solution 1:

(a) L.C.M. of 3 and 7 is 21

2 1 2 7 1 3   143 17

    

3 7 21 21 21

(b) L.C.M. of 10 and 15 is 30

3 7 3 3  7 2 9 14 23

    

10 15 30 30 30

4 2 4 7  2 9 28 18 46

    

9 7 63 63 63

(a) L.C.M. of 7 and 3 is 21

5 1 5 3  7 1 157 22 1

     1

7 3 21 21 21 21

(b) L.C.M. of 5 and 6 is 30

2 1 2 6  5 1 125 17

    

5 6 30 30 30

4 2 4 3  2 5 12 10 22 7

  =   1

5 3 15 15 15 15

(d) L.C.M. of 4 and 3 is 12

3 1 3 3  4 1 94 5

    

4 3 12 12 12

(e) L.C.M. of 6 and 3 is 6

5 1 5 1  2 1 52 3

      6 3 6 6 6

(f) L.C.M. of 3, 4 and 2 is 12

2 3 1 2 4    3 3 1 6 6 9 6 23 11

      1

3 4 2 12 12 12 12

(g) L.C.M. of 2, 3, and 6 is 6

1 1 1 1 3 1 2 1 1     3 2 1 6

      1

2 3 6 6 6 6

(h) L.C.M. of 3 and 3 is 3

4 11 4 11 15

     5

3 3 3 3

(i) L.C.M. of 3 and 4 is 12

14 13 14 4 13 3   5639 95 11

      7

3 4 12 12 12 12

(j) L.C.M. of 5 and 5 is 5

16 7 167 9 4     1

5 5 5 5 5

(k) L.C.M. of 3 and 2 is 6

4 1 4 2 1 3   83 5

     3 2 6 6 6

Question 2:

Sarika bought meter of ribbon and Lalita meter of ribbon. What is the total length of the ribbon they bought?

Solution 2:

Ribbon bought by Sarita = m and Ribbon bought by Lalita = m

2 3

Total length of ribbon = 

5 4

2 4  5 3

= [ L.C.M. of 5 and 4 is 20]

8 15 23 3

=  1 m

20 20 20

Therefore, they bought 1 m of ribbon.

Naina was given 1 piece of cake and Najma was given 1 piece of cake. Find the total amount of cake given to both of them.

Solution 3:

Cake taken by Naina = 1 piece and Cake taken by Najma = 1 piece

3 4

Total cake taken = 1 + 1 = 

2 3

3 3  4 2

98 17 5

=   2 [ L.C.M. of 2 and 3 is 6]

6 6 6

Therefore, the total consumption of cake is2 .

Question 4:

Fill in the boxes:

5 1 (a)  

8 4

1 1 (b)  

5 2

1 1

2 6

Solution 4:

1 5 25 7 (a)   

4 8 8 8

1 1 52 7 (b)    2 5 10 10

1 1 3 1 2 (c)   

2 6 6 6

Complete the addition – subtraction box:

(a) (b)

Solution 5:

Question 6:

A piece of wire meter long broke into two pieces. One piece was meter long. How long is the other piece?

Solution 6:

Total length of wire = meter

Length of first part = meter

7 1 7 1 2 1  

Remaining part = [ L.C.M. of 8 and 4 is 8]

8 4 8

=  meter 8 8

Therefore, the length of remaining part is meter.

Nandini house is km from her school. She walked some distance and then took a bus

for km to reach the school. How far did she walk?

Solution 7:

Total distance between school and house = km

Distance covered by bus = km

9 1 1 5  

Remaining distance = [ L.C.M. of 10 and 2 is 10]

Therefore, the distance covered by walking us km.

Question 8:

Ahsa and Samuel have bookshelves of the same size partly filled with books. Asha’s shelf is th full and Samuel’s shelf is th full. Whose bookshelf is more full? By what fraction?

Solution 8:

and

5 5 25 2 6 12

   and   [ L.C.M. of 6 and 5 is 30]

6 5 30 5 6 30

25 12



30 30

5 2   6 5

 Asha’s bookshelf is more covered than Samueal.

25 12 13 Difference =   30 30 30

Jaidev takes 2 minutes to walk across the school ground. Rahul takes minutes to do same. Who takes less time and by what fraction?

Solution 9:

Time taken by jaidev = 2 minutes = minutes

Time taken by Rahul = minutes

11 7 11 4  7 5

Difference =  = [ L.C.M. of 5 and 4 is 20]

5 4 20

4435 9

=  minutes 20 20

Thus, Rahul takes less time, which is minutes.

🌈⚡Key To Enjoy Learning Maths☘🌈

Pages