CONSECUTIVE NUMBERS

Place -1, -2, -3,-4,-5,-6,-7,-8 in these boxes so that the boxes which have consecutive numbers do not touch. 

They should not touch at all, not even at the corners. 
How many ways are possible?

Strategy to Solve:

To solve this, we need to:

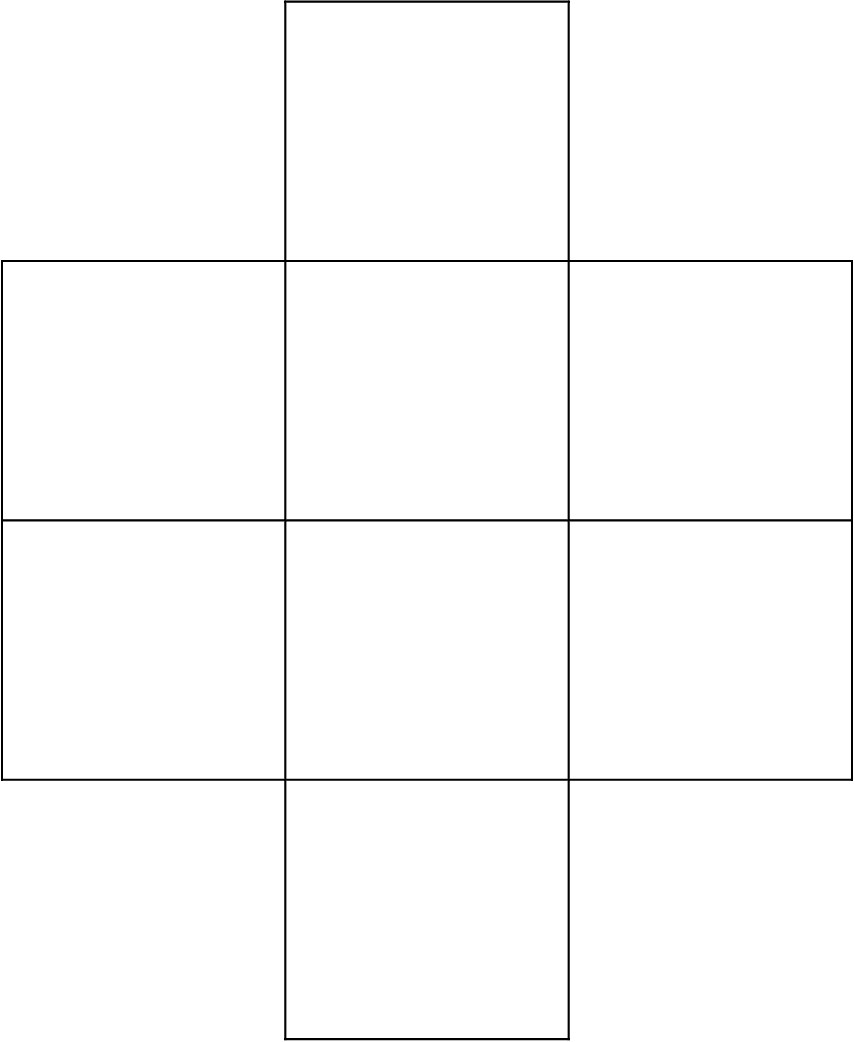
1. Model the adjacency of the 8 boxes using the image.

2. Generate all permutations of the numbers –1 to –8.

3. For each permutation:

   • Check that no two adjacent boxes contain consecutive numbers.

4. Count all valid arrangements.

Step-by-step Plan:

1. Number the boxes in the image (top to bottom, left to right) for easier referencing:

      [0]

[1][2][3]

[4][5][6]

      [7]

2. Define adjacency (touching at sides or corners):

const adjacency = {

  0: [1, 2, 3],

  1: [0, 2, 4, 5],

  2: [0, 1, 3, 4, 5, 6],

  3: [0, 2, 5, 6],

  4: [1, 2, 5, 7],

  5: [1, 2, 3, 4, 6, 7],

  6: [2, 3, 5, 7],

  7: [4, 5, 6]

};

3.Generate all 8! = 40320 permutations of the numbers –1 to –8.

4. Check each permutation:

• For each pair of adjacent boxes, check that their values are not consecutive (i.e. Math.abs(a - b) != 1).

Answer: 480 valid arrangements meet the puzzle's constraint.

🎲 Consecutive Negative Numbers Puzzle

Place the negative numbers from -1 to -8 into the boxes. The twist? No two consecutive numbers (e.g. -1 and -2) can be placed in adjacent boxes — even diagonally!

How to Play:

• Drag and drop numbers into the puzzle boxes.
• Consecutive numbers must NOT touch — not even corners!
• Click Check to validate your puzzle and receive a medal!

⏱ Time: 0 sec