Class 08 Activity – Understanding Quadrilaterals2

Objective: 

To verify that the sum of the measures of the exterior angles of any polygon is 360 ° by paper cutting and pasting.

Materials Requried : 

White sheets of paper, colour pencils, a pair of scissors, glue stick, geometry box, etc.

Procedure: 

(a) Triangle

On a white sheet of paper, draw a triangle ABC and produce its each side in order as shown below. Shade the exterior angles so formed using different colours.

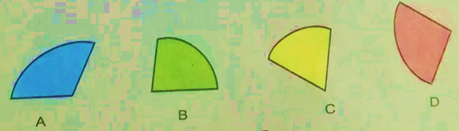
2. Using a pair of scissors, cut out the shaded angular regions.

3. Mark a point O on a white sheet of paper. Paste the three cut-outs such that the vertices of these angles coincide at O, as shown below.

While pasting these cut outs, it should be noted that no two cuts should overlap and there should not be any gap between them.

(b) Quadrilateral

1. On a white sheet of paper, draw a quadrilateral ABCD and produce its sides in order as shown below. Shade the exterior angles so formed using different colours.

2. Using a pair of scissors, cut out the four shaded angular regions.

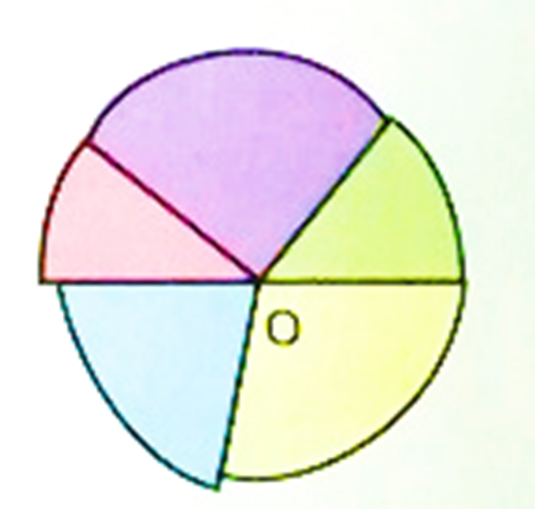
3. Mark a point on a white sheet of paper. Paste the four cut-outs such that the vertices of these angles (A, B, C, D,) coincide at O, as shown.

(c) Pentagon

On a white sheet of paper, draw a five sided polygon (pentagon) ABCDE and produce its sides in order. Shade of the exterior angles so formed using different colours. 

2. Using a pair of scissors, cut out the five shaded angular regions.

3. Mark a point O on a white sheet of paper. Paste the five cut-outs such that the vertices of these angles (A, B, C, D, E) coincide at O as shown.

(d) Hexagon

On a white sheet of paper, draw a 6 sided polygon (hexagon) ABCDEF and produce its sides in order. Shade the exterior angles so formed using different colours. 

2. Using a pair of scissors, cut out the six shaded angular regions.

3. Mark a point O of white sheet of paper.  Paste the six cut outs such that the vertices of these angles (A , B, C , D, E, F) coincide at O as shown in the fig.

Observations:

In figure, the three angular cut-outs together form a complete angle.

Thus, sum of the exterior angles of a triangle (3 sided polygon) is 360 °.

2. In figure, the four angular cut-outs together form a complete angle.

So, we can say that the sum of the exterior angles of a quadrilateral (four sided polygon) is 360°.

3. In figure, the five angular cut-outs together form a complete angle.

So, we can say that the sum of the exterior angles of a pentagon (5 sided polygon) is 360°.

4. In figure, the six angular cut-outs together form a complete angle.

So, we can say that the sum of the exterior angles of a hexagon (6 sided polygon) is 360°.

Conclusion: 

From the above activity, it is verified that the sum of the exterior angles of a polygon is 360°